题目内容
16.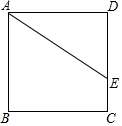 已知正方形ABCD中,点E在边DC上,DE=3,EC=1,如图所示,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为1或7.
已知正方形ABCD中,点E在边DC上,DE=3,EC=1,如图所示,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为1或7.
分析 首先在直角△ADE中利用勾股定理求得AE的长,然后分两种情况进行讨论,①当线段AE顺时针旋转时,在直角△ABF1中利用勾股定理求得BF1的长,进而求得F1C;
②同理可以求得旋转到F2时,F2C的长.
解答 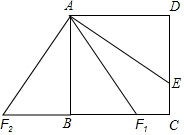 解:CD=DE+EC=3+1=4,则正方形ABCD的边长是4.
解:CD=DE+EC=3+1=4,则正方形ABCD的边长是4.
则在直角△ADE中,AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5.
①当线段AD顺时针旋转得到F1点,
AF1=AE=5,
在直角△ABF1中BF1=$\sqrt{A{{F}_{1}}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3.
∴F1C=BC-BF1=4-3=1;
②逆时针旋转得到F2点,同理可得BF2=3,则F2C=3+4=7.
故答案为1或7.
点评 本题考查了勾股定理以及图形的旋转,正确理解分两种情况进行讨论是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.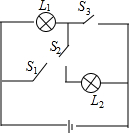 如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )
如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )
 如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )
如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{5}$ |
7.在Rt△ABC中,已知∠C=90°,AC=3,AB=4,则tanA的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{{\sqrt{7}}}{3}$ | D. | $\frac{{\sqrt{7}}}{4}$ |
1.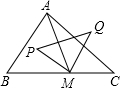 如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
 如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
5.关于单项式$\frac{{3{a^2}b}}{2}$,下列说法正确的是( )
| A. | 它与3πa2b是同类项 | B. | 它的系数是3 | ||
| C. | 它是二次单项式 | D. | 它与$-\frac{7}{2}{a^2}b$的和是2a2b |
 如图,一段抛物线:y=2x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至的C10,(1)请写出抛物线C2的解析式:y=-2(x-3)(x-6);(2)若P(17,m)在第10段抛物线C10上,则m=-260.
如图,一段抛物线:y=2x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至的C10,(1)请写出抛物线C2的解析式:y=-2(x-3)(x-6);(2)若P(17,m)在第10段抛物线C10上,则m=-260.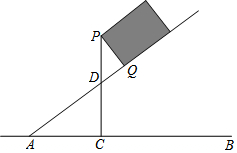 一长方形木箱沿斜面下滑,当木箱滑至如图所示位置时,AQ=m,己知木箱高PQ=h,斜面坡角α满足tanα=$\frac{3}{4}$(α为锐角),求木箱顶端P离地面AB的距离PC.
一长方形木箱沿斜面下滑,当木箱滑至如图所示位置时,AQ=m,己知木箱高PQ=h,斜面坡角α满足tanα=$\frac{3}{4}$(α为锐角),求木箱顶端P离地面AB的距离PC.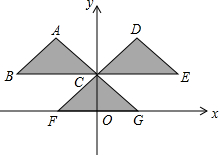 如图,三角形CFG的顶点坐标分别为C(0,$\frac{\sqrt{2}}{2}$),F(-$\frac{\sqrt{2}}{2}$,0),G($\frac{\sqrt{2}}{2}$,0).把三角形CFG平移两次,构成如图所示的图案(其中点B、C、E在一条平行于x轴的直线上).
如图,三角形CFG的顶点坐标分别为C(0,$\frac{\sqrt{2}}{2}$),F(-$\frac{\sqrt{2}}{2}$,0),G($\frac{\sqrt{2}}{2}$,0).把三角形CFG平移两次,构成如图所示的图案(其中点B、C、E在一条平行于x轴的直线上).