题目内容
10. 如图,已知D是△ABC内一点.
如图,已知D是△ABC内一点.(1)求作△ADE,使得D,E分别在AC的两侧,且AD=AE,∠DAE=∠BAC;
(2)在(1)的条件下,若AB=AC,连BD,EC,求证:BD=EC.
分析 (1)根据D,E分别在AC的两侧,且AD=AE,∠DAE=∠BAC,即可作出△ADE;
(2)根据∠DAE=∠BAC,得出∠BAD=∠CAE,再判定△ABD≌△ACE(SAS),即可得到BD=EC.
解答 解:(1)如图所示,△ADE即为所求;
(2)如图所示,连BD,EC,
∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS),
∴BD=EC.
点评 本题主要考查了复杂作图以及全等三角形的判定与性质,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
20.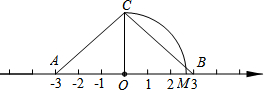 如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为( )
如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为( )
 如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为( )
如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为( )| A. | $\sqrt{7}$ | B. | 4 | C. | 5 | D. | 2.5 |
1.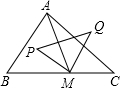 如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
 如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
如图,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是边BC上一动点,P、Q分别是△ABM、△ACM外接圆的圆心,则S△PMQ的最小值为6$\sqrt{3}$+12.
18.给出下列命题:①两边及一边上的中线对应相等的两个三角形全等;②底边和顶角对应相等的两个等腰三角形全等;③斜边和斜边上的高线对应相等的两个直角三角形全等,下列属于真命题的是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
5.关于单项式$\frac{{3{a^2}b}}{2}$,下列说法正确的是( )
| A. | 它与3πa2b是同类项 | B. | 它的系数是3 | ||
| C. | 它是二次单项式 | D. | 它与$-\frac{7}{2}{a^2}b$的和是2a2b |
15.已知(-1,y1),(1,y2)是直线y=-9x+6上的两个点,则y1,y2的大小关系是( )
| A. | y1>0>y2 | B. | y1>y2>0 | C. | y2>0>y1 | D. | 0>y1>y2 |
2.如果m表示有理数,那么|m|-m的值( )
| A. | 不可能是负数 | B. | 可能是零或者负数 | ||
| C. | 必定是零 | D. | 必定是正数 |
 如图,已知矩形ABCD中,FA、HB、FD、HC分别平分∠BAD、∠ABC、∠ADC、∠BCD.求证:四边形EFGH是正方形.
如图,已知矩形ABCD中,FA、HB、FD、HC分别平分∠BAD、∠ABC、∠ADC、∠BCD.求证:四边形EFGH是正方形.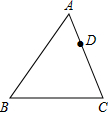 如图,在△ABC中,AB=8,AC=6,点D在AC上,AD=2,若点E在AB上,以A,D,E为顶点的三角形与△ABC相似.求AE的长.
如图,在△ABC中,AB=8,AC=6,点D在AC上,AD=2,若点E在AB上,以A,D,E为顶点的三角形与△ABC相似.求AE的长.