题目内容
11.若一个三角形的三边长的比为1:$\sqrt{3}$:2,则最小角的余弦值是$\frac{\sqrt{3}}{2}$.分析 根据一个三角形的三边长的比为1:$\sqrt{3}$:2,可以判断这个三角形的形状,然后根据大边对大角,可知最小的角是比值中1所对的角,从而可以得到最小角的余弦值.
解答 解:∵一个三角形的三边长的比为1:$\sqrt{3}$:2,
∴设这个三角形的三边长为:x,$\sqrt{3}x,2x$,
∵${x}^{2}+(\sqrt{3})^{2}={x}^{2}+3{x}^{2}=4{x}^{2}$,(2x)2=4x2
∴此三角形是直角三角形,
∴最小角的余弦值是:$\frac{\sqrt{3}}{2}$,
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查解直角三角形,勾股定理的逆定理,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
1. 如图,直角三角形ABC沿直角边BC所在的直线向右平移到△DEF处,那么,下列结论中错误的是( )
如图,直角三角形ABC沿直角边BC所在的直线向右平移到△DEF处,那么,下列结论中错误的是( )
 如图,直角三角形ABC沿直角边BC所在的直线向右平移到△DEF处,那么,下列结论中错误的是( )
如图,直角三角形ABC沿直角边BC所在的直线向右平移到△DEF处,那么,下列结论中错误的是( )| A. | AC=DF | B. | ∠DEF=90° | C. | △ABC≌△DEF | D. | EC=CF |
6.己知代数式2y2+3y+7的值是8,则代数式4y2+6y-9的值是( )
| A. | 2 | B. | 17 | C. | 7 | D. | -7 |
16.下列几组数能作为直角三角形的三边长的是( )
| A. | 2,2,$\sqrt{8}$ | B. | $\sqrt{3}$,2,$\sqrt{5}$ | C. | 9,12,18 | D. | 12,15,20 |
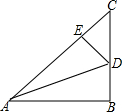 如图,在△ABC中,∠B=90°,AB=BC=4,点D在BC上,将△ABC沿AD折叠,使点B落在AC边上的点E处.
如图,在△ABC中,∠B=90°,AB=BC=4,点D在BC上,将△ABC沿AD折叠,使点B落在AC边上的点E处. 如图,一观测塔底座部分是四棱柱,现在从下底面A点修建钢筋扶梯,经过点M、N到点D′,再进入顶部的观测室,已知AB=BC=CD=3米,高AA′=9米,问点M、N位于什么位置,才能使扶梯的总长度最小,从而造价最低?
如图,一观测塔底座部分是四棱柱,现在从下底面A点修建钢筋扶梯,经过点M、N到点D′,再进入顶部的观测室,已知AB=BC=CD=3米,高AA′=9米,问点M、N位于什么位置,才能使扶梯的总长度最小,从而造价最低? 某地区随机抽查了一部分市民进行法律知识测试,测试成绩(得分取整数,每组数据含最小值不含最大值)整理后,得到如图所示的频数分布直方图,写出一条你从图中所获得的信息:分数在70~80之间的人数最多;成绩低于60分的有3人;成绩90分及其以上的有6人;参加测试的共有48人等.
某地区随机抽查了一部分市民进行法律知识测试,测试成绩(得分取整数,每组数据含最小值不含最大值)整理后,得到如图所示的频数分布直方图,写出一条你从图中所获得的信息:分数在70~80之间的人数最多;成绩低于60分的有3人;成绩90分及其以上的有6人;参加测试的共有48人等.