Question

2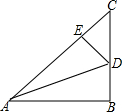．如图，在△ABC中，∠B=90°，AB=BC=4，点D在BC上，将△ABC沿AD折叠，使点B落在AC边上的点E处．
（1）判断△CDE是什么特殊三角形，并说明理由；
（2）求线段BD的长．

Answer 1

分析 （1）根据等腰直角三角形的性质得到∠C=45°，根据折叠的性质得到∠AED=∠B=90°，可以得到结论．
（2）由折叠的性质得BD=DE，AE=AB=4，∠AED=∠B=90?，设DE=DB=EC=x，则CD=（4-x），在Rt△CED中依据勾股定理列方程求解即可．

解答 解：（1）∵AB=BC，∠B=90°，
∴∠C=45°，
由折叠可知∠CED=90°，
∴∠CED=∠C=45°，
∴△CDE是等腰直角三角形．
（2）设BD=x，则DE=CD=x，
由勾股定理得到CD=$\sqrt{2}$x，
∵BC=4，
∴$\sqrt{2}$x+x=4，
∴x=$\frac{4}{\sqrt{2}+1}$=4$\sqrt{2}$-4，
即BD=4$\sqrt{2}$-4．

点评 本题考查了翻折变换的性质，勾股定理，主要利用了翻折前后的两个图形对应边相等，对应角相等，利用勾股定理列出关于x的方程是解题的关键