题目内容
6．己知代数式2y2+3y+7的值是8，则代数式4y2+6y-9的值是（ ）| A． | 2 | B． | 17 | C． | 7 | D． | -7 |
分析 将2y2+3y+7=8变形后代入，即可得出答案．
解答 解：∵2y2+3y+7=8
∴2y2+3y=1
∴4y2+6y-9=2（2y2+3Y）-9=2-9=-7
故选D．
点评 本题考查了求代数式的值的应用，用了整体代入思想．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
14．
在下列网格中，小正方形的边长为1，点A、B、O都在格点上，则∠A的正弦值是（ ）
在下列网格中，小正方形的边长为1，点A、B、O都在格点上，则∠A的正弦值是（ ）| A． | $\frac{\sqrt{5}}{5}$ | B． | $\frac{\sqrt{5}}{10}$ | C． | $\frac{2\sqrt{5}}{5}$ | D． | $\frac{1}{2}$ |
1．
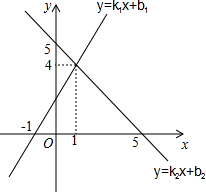已知函数y=k1x+b1与函数y=k2x+b2的图象如图所示，则方程组$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}-y=0}\\{{k}_{2}x+{b}_{2}-y=0}\end{array}\right.$的解为（ ）
已知函数y=k1x+b1与函数y=k2x+b2的图象如图所示，则方程组$\left\{\begin{array}{l}{{k}_{1}x+{b}_{1}-y=0}\\{{k}_{2}x+{b}_{2}-y=0}\end{array}\right.$的解为（ ）| A． | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=-1}\\{y=5}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=5}\\{y=5}\end{array}\right.$ |
18．已知点（-3，y1），（1，y2）都在直线y=kx+2（k＜0）上，则y1，y2大小关系是（ ）
| A． | y1＞y2 | B． | y1=y2 | C． | y1＜y2 | D． | 不能比较 |
小明用若干个正方形和长方形准备拼成一个长方体的展开图，拼完后，小明看来看去觉得所拼图形似乎存在问题．
16．如图，有6张扑克牌，从中随机抽取一张，点数小于7的可能性大小是（ ）
| A． | 3 | B． | $\frac{1}{2}$ | C． | 1 | D． | $\frac{1}{3}$ |