题目内容
12.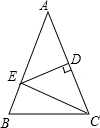 如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.(1)求∠BEC的度数.
(2)若CE=5,求BC的长.
分析 (1)ED是AC的垂直平分线,可得AE=EC;∠A=∠ACE;已知∠A=36,可求∠ACE,再根据三角形外角的性质即可求解;
(2)根据等腰三角形性质和三角形内角和定理求出∠B=∠ACB=72°,求出∠BEC=∠B,推出BC=CE即可.
解答 解:(1)∵DE垂直平分AC,
∴CE=AE,
∴∠ECD=∠A=36°,
∴∠BEC=∠A+∠ECD=36°+36°=72°;
(2)∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∴∠BEC=∠A+∠ECD=72°,
∴∠BEC=∠B,
∴BC=EC=5.
点评 本题考查了线段垂直平分线,三角形内角和定理,等腰三角形性质,三角形外角的性质的应用,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知G是△ABC的重心,且GP∥BC交AB于点P,BC=3$\sqrt{3}$,则GP的长为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
 如图,AE是△BAC的平分线,ED⊥AB于E,EF⊥AC于F,S△ABC=9,DE=2,AB=4,则AC的长为5.
如图,AE是△BAC的平分线,ED⊥AB于E,EF⊥AC于F,S△ABC=9,DE=2,AB=4,则AC的长为5.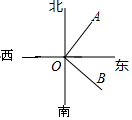 如图,在点O北偏东65°的某处有一点A,在点O南东20°的某处有一点B,则∠AOB的度数是95°.
如图,在点O北偏东65°的某处有一点A,在点O南东20°的某处有一点B,则∠AOB的度数是95°. 王鹏家里购买了一套小户型商品房,准备将地面铺上相同的地砖,地面结构如下图,根据图中的数据(单位:m),解答下列问题.
王鹏家里购买了一套小户型商品房,准备将地面铺上相同的地砖,地面结构如下图,根据图中的数据(单位:m),解答下列问题. 如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.