题目内容
△ABC的面积是60cm2，D、E分别是AC、AB边上一点，且AD=2DC，BE=3AE，BD与EC交于点O，求四边形AEOD的面积．考点：三角形的面积
专题：
分析：根据等高的三角形面积比等于底边比，可得S△AED，S△EDB，S△EDC，S△EBC，从而得到
的值，进一步得到S△EOD，再根据和差关系即可得到四边形AEOD的面积．
| DO |
| BO |
解答：
解：连结DE．
∵△ABC的面积是60cm2，AD=2DC，BE=3AE，
∴S△AED=10cm2，S△EDB=30cm2，S△EDC=5cm2，S△EBC=45cm2，
∴
=
=
，
∴S△EOD=
×S△EDB=3cm2，
S四边形AEOD=S△AED+S△EOD=10+3=3cm2．
解：连结DE．∵△ABC的面积是60cm2，AD=2DC，BE=3AE，
∴S△AED=10cm2，S△EDB=30cm2，S△EDC=5cm2，S△EBC=45cm2，
∴
| DO |
| BO |
| 5 |
| 45 |
| 1 |
| 9 |
∴S△EOD=
| 1 |
| 1+9 |
S四边形AEOD=S△AED+S△EOD=10+3=3cm2．
点评：考查了三角形的面积，关键是熟练掌握等高的三角形面积比等于底边比的性质．
练习册系列答案
相关题目
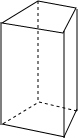观察如图所示的直四棱柱．
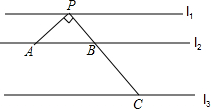如图，直线l1∥l2∥l3，l1与l2之间的距离为1，l2与l3之间的距离为2，点P在l1上，点A在l2上，点C在l3上，PC交l2于点B，PA⊥PC．
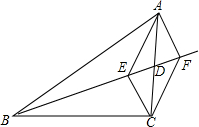如图，BD是△ABC的中线，CE⊥BD于点E，AF⊥BD交BD的延长线于点F．
直线y=2x+3与直线y=-2x-1的图象如图所示．