题目内容
已知△ABC中，AD为中线，E、F分别在AB、AC上，且AE=AF，EF交AD于G，求证：
=
．
| GE |
| GF |
| AC |
| AB |
考点：相似三角形的判定与性质
专题：证明题
分析：过G分别作AB，AC的垂线，垂足分别为H，I，由△GHE∽△GFI，得出
=
，由D是BC中点，得出S△ABD=S△ACD，可得出S△ABG=S△ACG，由AB•GH=AC•GI，即
=
，即可得出结论经．
| GH |
| GI |
| GE |
| GF |
| GH |
| GI |
| AC |
| AB |
解答：证明：如图，过G分别作AB，AC的垂线，垂足分别为H，I
∵AE=AF，
∴∠AEG=∠AFG，
∴△GHE∽△GFI，
∴
=
，
∵D是BC中点，
∴S△ABD=S△ACD，
∴S△ABG=S△ACG，
∴AB•GH=AC•GI，即
=
∴
=
．
∵AE=AF，
∴∠AEG=∠AFG，
∴△GHE∽△GFI，
∴
| GH |
| GI |
| GE |
| GF |
∵D是BC中点，
∴S△ABD=S△ACD，
∴S△ABG=S△ACG，
∴AB•GH=AC•GI，即
| GH |
| GI |
| AC |
| AB |
∴
| GE |
| GF |
| AC |
| AB |
点评：本题主要考查了相似三角形的判定与性质，解题的关键是得出S△ABG=S△ACG．
练习册系列答案
相关题目
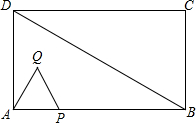如图，在△ABD中，∠DAB=90°，∠ABD=30°，AD=2
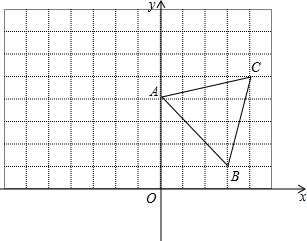已知在平面直角坐标系中，点A的坐标为（0，4），点B的坐标为（3，1），点C的坐标为（4，5），将△ABC绕原点O逆时针旋转90°，得到△A1B1C1，（其中点A转到点A1处，点B转到点B处）．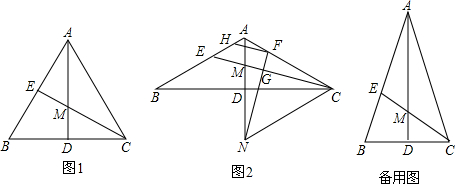
△ABC的面积是60cm2，D、E分别是AC、AB边上一点，且AD=2DC，BE=3AE，BD与EC交于点O，求四边形AEOD的面积．