题目内容
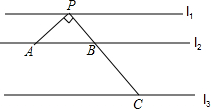如图，直线l1∥l2∥l3，l1与l2之间的距离为1，l2与l3之间的距离为2，点P在l1上，点A在l2上，点C在l3上，PC交l2于点B，PA⊥PC．（1）当PA=3时，求PC的长；
（2）在∠APC绕点P旋转的过程中，△ABC是否可能是等腰三角形？如果可能，请求出PC的长；如果不能，请说明理由．
考点：相似三角形的判定与性质,等腰三角形的判定,勾股定理
专题：
分析：（1）过P作PD⊥L3，交L2于E，交L3于D．利用条件可得△PAE∽△BPE和△PEB∽△PDC，代入可求出PC的长度；
（2）由等腰三角形，可得△ABP≌BCF，再利用三角函数的定义可求出PC的长．
（2）由等腰三角形，可得△ABP≌BCF，再利用三角函数的定义可求出PC的长．
解答：解：
（1）过P作PD⊥L3，交L2于E，交L3于D．
则AE2═PA2-PE2═32-12═8，AE═2
，
∵△PAE∽△BPE，
∴
=
，
∴
=
，
∴PB=
，
又∵△PEB∽△PDC，
∴
=
，
∴
=
，
∴PC═
；
（2）可能．
当△ABC为等腰三角形时，因为∠ABC为钝角，所以只能有AB═BC．过B作BF⊥L3于F，则△ABP≌BCF，
∴PA═BF═2
∴△ABP的斜边的高为1，则∠PAB═30°，
∴∠FBC═60°，
∴Sin60°=
，
∴PC═
=
=2
．
（1）过P作PD⊥L3，交L2于E，交L3于D．
则AE2═PA2-PE2═32-12═8，AE═2
| 2 |
∵△PAE∽△BPE，
∴
| PA |
| PB |
| AE |
| PE |
∴
| 3 |
| PB |
2
| ||
| 1 |
∴PB=
3
| ||
| 4 |
又∵△PEB∽△PDC，
∴
| PE |
| PD |
| PB |
| PC |
∴
| 1 |
| 3 |
| ||||
| PC |
∴PC═
9
| ||
| 4 |
（2）可能．
当△ABC为等腰三角形时，因为∠ABC为钝角，所以只能有AB═BC．过B作BF⊥L3于F，则△ABP≌BCF，
∴PA═BF═2
∴△ABP的斜边的高为1，则∠PAB═30°，
∴∠FBC═60°，
∴Sin60°=
| 3 |
| PC |
∴PC═
| 3 |
| sin60° |
| 3 | ||||
|
| 3 |
点评：本题主要考查相似三角形的判定和性质，解题的关键是作出辅助线构造三角形相似．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
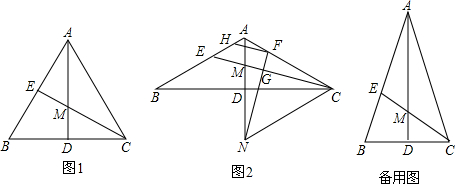
正方形ABCD中，E是BC延长线上的点，BF⊥DE于F，连接AF，探究线段AF、BF、DF的数量关系．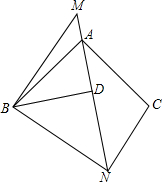
如图，已知△ABC和△MBN都是等腰直角三角形，∠BAC=∠MBN=90°，BD⊥AN．请找出与△ABD相似的三角形并给出证明，直接写出∠ANC的度数．
△ABC的面积是60cm2，D、E分别是AC、AB边上一点，且AD=2DC，BE=3AE，BD与EC交于点O，求四边形AEOD的面积．