题目内容
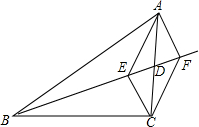 如图,BD是△ABC的中线,CE⊥BD于点E,AF⊥BD交BD的延长线于点F.
如图,BD是△ABC的中线,CE⊥BD于点E,AF⊥BD交BD的延长线于点F.(1)求证:DE=DF;
(1)求证:BE+BF=2BD;
(2)连AE、CF,求证:AE∥CF.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)根据三角形中线的定义可得AD=CD,根据垂直的定义可得∠CED=∠AFD=90°,然后利用“角角边”证明△CDE和△ADF全等,根据全等三角形对应边相等可得DE=DF;
(2)用BD表示出BE、BF,然后整理即可得证;
(3)根据对角线互相平分的四边形是平行四边形得到四边形AECF是平行四边形,再根据平行四边形的对边平行证明即可.
(2)用BD表示出BE、BF,然后整理即可得证;
(3)根据对角线互相平分的四边形是平行四边形得到四边形AECF是平行四边形,再根据平行四边形的对边平行证明即可.
解答:(1)证明:∵BD是△ABC的中线,
∴AD=CD,
∵CE⊥BD,AF⊥BD,
∴∠CED=∠AFD=90°,
在△CDE和△ADF中,
,
∴△CDE≌△ADF(AAS),
∴DE=DF;
(2)∵BE=BD-DE,
BF=BD+DF,
∴BE+BF=BD-DE+BD+DF=2BD,
即BE+BF=2BD,
(3)∵AD=CD,DE=DF,
∴四边形AECF是平行四边形,
∴AE∥CF.
∴AD=CD,
∵CE⊥BD,AF⊥BD,
∴∠CED=∠AFD=90°,
在△CDE和△ADF中,
|
∴△CDE≌△ADF(AAS),
∴DE=DF;
(2)∵BE=BD-DE,
BF=BD+DF,
∴BE+BF=BD-DE+BD+DF=2BD,
即BE+BF=2BD,
(3)∵AD=CD,DE=DF,
∴四边形AECF是平行四边形,
∴AE∥CF.
点评:本题考查了全等三角形的判定与性质,三角形中线的定义,平行四边形的判定与性质,熟练掌握三角形全等的判定方法并准确识图找出三角形全等的条件是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 已知,如图,OE平分∠AOB,BC、AD分别垂直于OA、OB,求证:EC=DE.
已知,如图,OE平分∠AOB,BC、AD分别垂直于OA、OB,求证:EC=DE.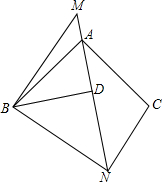 如图,已知△ABC和△MBN都是等腰直角三角形,∠BAC=∠MBN=90°,BD⊥AN.请找出与△ABD相似的三角形并给出证明,直接写出∠ANC的度数.
如图,已知△ABC和△MBN都是等腰直角三角形,∠BAC=∠MBN=90°,BD⊥AN.请找出与△ABD相似的三角形并给出证明,直接写出∠ANC的度数.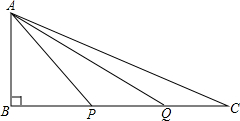 如图,△ABC中,∠ABC=90°,点P、Q分别是边BC上的两点,连接AP、AQ,且AB=BP=PQ=QC=1,问图中是否有相似三角形?并说明理由.
如图,△ABC中,∠ABC=90°,点P、Q分别是边BC上的两点,连接AP、AQ,且AB=BP=PQ=QC=1,问图中是否有相似三角形?并说明理由. △ABC的面积是60cm2,D、E分别是AC、AB边上一点,且AD=2DC,BE=3AE,BD与EC交于点O,求四边形AEOD的面积.
△ABC的面积是60cm2,D、E分别是AC、AB边上一点,且AD=2DC,BE=3AE,BD与EC交于点O,求四边形AEOD的面积.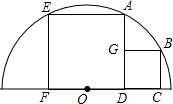 四边形ADFE和四边形BCDG都为正方形,且点F、D、C在半圆O的直径上,点E、A、B在半圆O的圆弧上,若小正方形边长为4cm,求该半圆的半径.
四边形ADFE和四边形BCDG都为正方形,且点F、D、C在半圆O的直径上,点E、A、B在半圆O的圆弧上,若小正方形边长为4cm,求该半圆的半径. 在△ABC中,M是BC边的中点,D是AC上一点,BD与AM交于点E,且DA=DE.求证:BE=AC.
在△ABC中,M是BC边的中点,D是AC上一点,BD与AM交于点E,且DA=DE.求证:BE=AC.