题目内容
13. 如图.在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的与反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于二、四象限A(-4,3),B(6,n)的点.
如图.在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的与反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于二、四象限A(-4,3),B(6,n)的点.(1)求反比例函数和一次函数的解析式;
(2)当x满足什么条件时,y1>y2?
分析 (1)将点A的坐标代入反比例函数的解析式可得k2=4,进而求得:m=-12,即A(-4,3),B(6,-2)在直线y1=kx+b上,将其坐标代入即求可得一次函数的解析式.
(2)已知两函数的解析式、图象,易得y1与y2的大小关系.
解答 解:(1)∵A(-4,3)在y=$\frac{m}{x}$上
∴3=$\frac{m}{-4}$,
m=-12
∵B(6,n)在y=-$\frac{12x}{\;}$上
所以n=-$\frac{12}{6}$,
∴n=-2,
∴B(6,-2)
∴$\left\{\begin{array}{l}{3=-4k+3}\\{-2=6k+3}\end{array}\right.$,
解后得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=1}\end{array}\right.$,
∴${y}_{1}=-\frac{1}{2}x+1$,${y}_{2}=-\frac{12}{x}$;
(2)当x<-4或0<<2时,y1>y2.
点评 本题考查了反比例函数与一次函数的交点问题,待定系数法求反比例函数与一次函数的解析式,也考查了观察函数图象的能力.

练习册系列答案
相关题目
3.若a、b互为相反数,则( )
| A. | ab>0 | B. | ab<0 | C. | ab≥0 | D. | ab≤0 |
2. 如图,将Rt△ABC,其中∠B=30°,∠C=90°,AC=1,绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么,点B所运动的路径长( )
如图,将Rt△ABC,其中∠B=30°,∠C=90°,AC=1,绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么,点B所运动的路径长( )
 如图,将Rt△ABC,其中∠B=30°,∠C=90°,AC=1,绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么,点B所运动的路径长( )
如图,将Rt△ABC,其中∠B=30°,∠C=90°,AC=1,绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么,点B所运动的路径长( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | $\frac{4π}{3}$ | D. | $\frac{2\sqrt{3}π}{3}$ |
 一架云梯长10m,如图所示斜靠在一面墙上,梯子底端C离墙6m.
一架云梯长10m,如图所示斜靠在一面墙上,梯子底端C离墙6m. 如图,用一个平面从正方体的三个顶点处截去正方体的一角变成一个新的多面体,这个多面体共有12条棱.
如图,用一个平面从正方体的三个顶点处截去正方体的一角变成一个新的多面体,这个多面体共有12条棱. ”可爱吧!表面能展开平面图形“
”可爱吧!表面能展开平面图形“ ”的是圆锥..
”的是圆锥..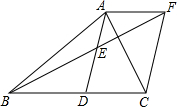 如图,在△ABC中,AD是BC边的中线,E是AD的中点,过A点作AF∥BC交BE的延长线于点F,连结CF.求证:四边形ADCF是平行四边形.
如图,在△ABC中,AD是BC边的中线,E是AD的中点,过A点作AF∥BC交BE的延长线于点F,连结CF.求证:四边形ADCF是平行四边形.