题目内容
15.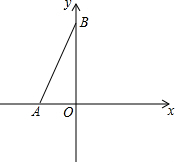 如图,在平面直角坐标系中,A(a,0),B(0,b),且a,b满足|a+b-4|+(2a+4)2=0.
如图,在平面直角坐标系中,A(a,0),B(0,b),且a,b满足|a+b-4|+(2a+4)2=0.(1)求OA,OB的长度;
(2)若P从点B出发沿着射线BO方向(点P不与原点重合),速度为每秒2个单位长度,连接AP,设点P的运动时间为t,△AOP的面积为S,请你用含t的式子表示S;
(3)在(2)的条件下,当S=4时,在一、三象限角平分线上是否存在一点M(点M不与原点重合),使得PM⊥AM?若存在,求M点坐标;若不存在,请说明理由.
分析 (1)根据解方程组,可得a、b的值;
(2)根据三角形的面积公式,可得答案;
(3)根据互相垂直两直线的一次项系数的乘积为-1,可得关于a的方程,根据解方程,可得答案.
解答 解:(1)由a,b满足|a+b-4|+(2a+4)2=0,得
$\left\{\begin{array}{l}{a+b-4=0}\\{2a+4=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-2}\\{b=6}\end{array}\right.$,
OA=|a|=2,OB=|b|=6;
(2)如图: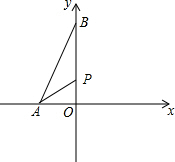
BP=2t,OP=OB-BP=b-2t=6-2t,OA=2,
S=$\frac{1}{2}$OP•OA=$\frac{1}{2}$×2×(6-2t)=6-2t;
(3)不存在M点使PM⊥AM,理由如下:
设M(a,a),假设PM⊥AM,
当S=4时,2t=4,解得t=2,
P(0,2),A(-2,0).
由PM⊥AM,得$\frac{a-2}{a}$•$\frac{a-0}{a+2}$=-1.
解得a=0,
即M点坐标为(0,0),
∵M点原点不重合,
∴M点不存在.
点评 本题考查了一次函数综合题,利用了解方程得出a、b的值,三角形的面积公式,利用互相垂直两直线的一次项系数的乘积为-1得出关于a的方程是解题关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
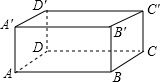 有一个长方形纸盒,长、宽、高分别为4cm、3cm、12cm,请你算一算,能否把一根长为18cm的铅笔放入这个纸盒里面?
有一个长方形纸盒,长、宽、高分别为4cm、3cm、12cm,请你算一算,能否把一根长为18cm的铅笔放入这个纸盒里面?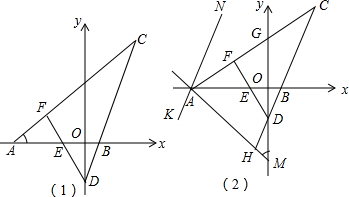
 已知直线y=$\frac{3}{4}$x+3分别交x轴、y轴于点A、B.
已知直线y=$\frac{3}{4}$x+3分别交x轴、y轴于点A、B.