题目内容
16．
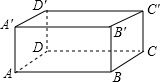有一个长方形纸盒，长、宽、高分别为4cm、3cm、12cm，请你算一算，能否把一根长为18cm的铅笔放入这个纸盒里面？
分析 长方体内体对角线是最长的，当木条在盒子里对角放置时，木棒长度的长度最大，所以求出盒子的对角线长度与18cm比较即可．
解答 解：
由题意得：AC2=AB2+BC2，AC′2=AC2+CC′2，
故AC′2=AB2+BC2+CC′2，
从而可得对角线长度AC′=$\sqrt{A{C}^{2}+CC{′}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13（cm）．
故不能将一根长为18cm的铅笔放入这个盒子里面．
点评 本题考查了学生的空间想象能力及勾股定理的应用，解题的关键是熟悉勾股定理并两次应用勾股定理．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
1．若x1和x2是下列方程的两个根．请你完成下表；
（1）探究猜想．你能得到什么结论？
（2）根据上面你发现的结论．求解下面的问题：已知方程x2+3x-5=0的两个根分别为x1．x2 求$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值．
| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| x2-5x+4=0 | 1 | 4 | 5 | 4 |
| x2+7x+12=0 | -3 | -4 | -7 | 12 |
| x2-4x-5=0 | 5 | -1 | 4 | -5 |
| x2+bx+c=0 | $\frac{-b+\sqrt{{b}^{2}-4c}}{2}$ | $\frac{-b-\sqrt{{b}^{2}-4c}}{2}$ | -b | c |
（2）根据上面你发现的结论．求解下面的问题：已知方程x2+3x-5=0的两个根分别为x1．x2 求$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值．
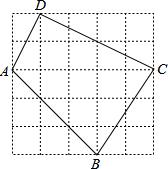如图，每个小方格都是边长为1的正方形．
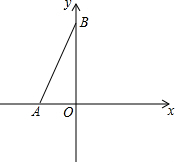如图，在平面直角坐标系中，A（a，0），B（0，b），且a，b满足|a+b-4|+（2a+4）2=0．