题目内容
5.如图,在10×6的正方形网格中,每个小正方形的边长均为1,线段AB的端点A、B均在格点上.分别在图甲和图乙中作出以AB为一腰的等腰△ABC,使其顶角分别为直角和钝角,点C在格点上,并直接写出△ABC的周长.图甲:△ABC的周长=10+5$\sqrt{2}$.图乙:△ABC的周长=10+4$\sqrt{5}$.
分析 根据题意画出图形,再由勾股定理求出各边的长,进而可得出结论.
解答  解:如图甲所示,△ABC的周长=5+5+$\sqrt{{5}^{2}+{5}^{2}}$=10+5$\sqrt{2}$;
解:如图甲所示,△ABC的周长=5+5+$\sqrt{{5}^{2}+{5}^{2}}$=10+5$\sqrt{2}$;
如图乙所示,△ABC的周长=5+5+$\sqrt{{4}^{2}+{8}^{2}}$=10+4$\sqrt{5}$.
故答案为:10+5$\sqrt{2}$,10+4$\sqrt{5}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
13.已知$\frac{1}{x}-\frac{1}{y}=3$,则分式$\frac{2x+3xy-2y}{x-2xy-y}$的值为( )
| A. | $\frac{3}{5}$ | B. | 9 | C. | 1 | D. | 不能确定 |
10.一次函数y=2x+4的图象与x轴的交点坐标是( )
| A. | (-2,0) | B. | (0,-2) | C. | (4,0) | D. | (0,4) |
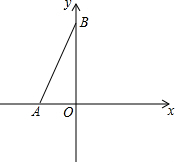 如图,在平面直角坐标系中,A(a,0),B(0,b),且a,b满足|a+b-4|+(2a+4)2=0.
如图,在平面直角坐标系中,A(a,0),B(0,b),且a,b满足|a+b-4|+(2a+4)2=0.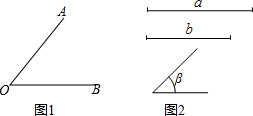 尺规作图(请保留作图痕迹,不写作法).
尺规作图(请保留作图痕迹,不写作法).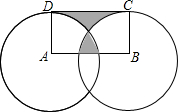 如图,分别以矩形ABCD的顶点A和B为圆心,作半径为1的两个圆正好分别经过C、D两点,若图中两块阴影部分的面积相等,则AB的长度是$\frac{π}{2}$.
如图,分别以矩形ABCD的顶点A和B为圆心,作半径为1的两个圆正好分别经过C、D两点,若图中两块阴影部分的面积相等,则AB的长度是$\frac{π}{2}$.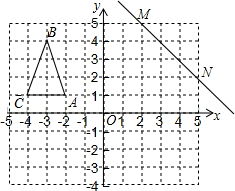 如图,在直角坐标系中有一个格点三角形ABC(顶点都在格点上的三角形),已知A(-2,1),B(-3,4),C(-4,1),直线MN过点M(2,5),N(5,2).
如图,在直角坐标系中有一个格点三角形ABC(顶点都在格点上的三角形),已知A(-2,1),B(-3,4),C(-4,1),直线MN过点M(2,5),N(5,2).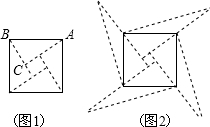 图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )