题目内容
4.已知关于x的方程x2-(k+2)x+2k=0(1)试判断方程根的情况;
(2)若这个方程与方程x2-(k-2)x-4=0有一个相同的根,求k的值.
分析 (1)先找出a=1,b=-(k+2),c=2k,求出根的判别式,即可判断方程根的情况;
(2)首先求出方程x2-(k+2)x+2k=0两根,然后分别把两根代入方程x2-(k-2)x-4=0,进而求出k的值.
解答 解:(1)∵a=1,b=-(k+2),c=2k,
∴△=b2-4ac=(k+2)2-8k=(k-2)2≥0,
∴方程总有实数根;
(2)方程x2-(k+2)x+2k=0两根为2和k,
当x=2也是方程x2-(k-2)x-4=0有一个相同的根时,
则4-2k+4-4=0,解得k=2,
当x=k也是方程x2-(k-2)x-4=0有一个相同的根时,
则k2-k2+2k-4=0,解得k=2,
综上k的值为2.
点评 本题主要考查了根的判别式以及一元二次方程的解的知识,解答本题要掌握一元二次方程根的情况与判别式△的关系:△≥0时方程有实数根.

练习册系列答案
相关题目
12.下列一元二次方程中,有两个相等的实数根的是( )
| A. | x2+2x-1=0 | B. | x2-6x+9=0 | C. | x2+4x+2=0 | D. | -x2+x+2=0 |
13.已知$\frac{1}{x}-\frac{1}{y}=3$,则分式$\frac{2x+3xy-2y}{x-2xy-y}$的值为( )
| A. | $\frac{3}{5}$ | B. | 9 | C. | 1 | D. | 不能确定 |
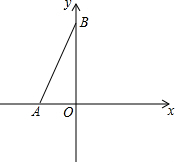 如图,在平面直角坐标系中,A(a,0),B(0,b),且a,b满足|a+b-4|+(2a+4)2=0.
如图,在平面直角坐标系中,A(a,0),B(0,b),且a,b满足|a+b-4|+(2a+4)2=0.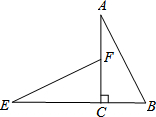 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=$\sqrt{5}$,BC=1,则线段BE的长为3,顶点A所运动过的路程等于π(保留π).
如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=$\sqrt{5}$,BC=1,则线段BE的长为3,顶点A所运动过的路程等于π(保留π).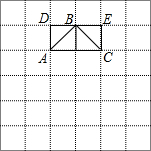 阅读并解决问题
阅读并解决问题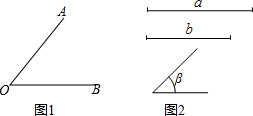 尺规作图(请保留作图痕迹,不写作法).
尺规作图(请保留作图痕迹,不写作法).