��Ŀ����
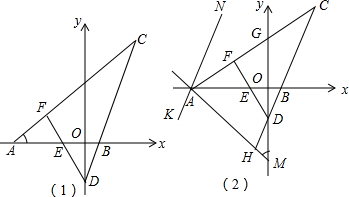
3����ͼ����֪����ƽ��ֱ������ϵ�У�A��a��0����B��b��0����a��0��b��0����1������C��y��������|a+4|+��b-2��2=0����ABC�����Ϊ18����C������ꣻ
��2����C���ڵ�һ�����˶���CA��y����G�㣬CB���ӳ��߽�y����D�㣬E��ΪB�����y��ĶԳƵ㣬DE���ӳ��߽�AC��F�㣬
�ٵ���DFC=��C+70��ʱ�����BAC�Ķ�����
�ڽ��߶�DCƽ�ƣ�ʹ�侭��A����߶�NK����A��ֱ��AM��y����M����CD�ӳ���H�㣬�������CAH=��CHAʱ��$\frac{��AMO}{��DFC}$��ֵ��
���� ��1������ż�η��Լ�����ֵ�����ʵó�A��B�����꣬����������������ó�C�����ꣻ
��2����������������ǵ����ʵó���BAC+��BAC+��C=��DFC�������ó���CBA+��CAB+��C=��C+70��������ɣ�
�ڽ����֪������������ǵ����ʵó�����CFD=180��-��C-2��ODB����DMA=��AMO=90��-$\frac{1}{2}$��C-��ODB�������ó��𰸣�
���  �⣺��1����ͼ1��ʾ��
�⣺��1����ͼ1��ʾ��
��|a+4|+��b-2��2=0��
��a=-4��b=2��
��A��-4��0����B��2��0����
�ߵ�C��y���ϣ���ABC�����Ϊ18��
��AB=6����CO=6��
��C��0��6����0��-6����
��2������ͼ��1����
�ڡ�ABC�У���EBD=��CAB+��C��
��OE=OB����BED=��EBD��
���BED=��CAB+��C��
�֡ߡ�AEF=��BED��
���ڡ�AFE�У���BAC+��AEF=��DFC��
���BAC+��BAC+��C=��DFC��
�֡ߡ�DFC=��C+70�㣬
��CBA+��CAB+��C=��C+70�㣬
���BAC=35�㣻
����ͼ��2����
�ڡ�CFD�У���E��ΪB�����y��ĶԳƵ㣬
���EDB=��ODB��
���CFD=180��-��C-2��ODB��
�ڡ�DMH�У���DMA=��CHA-��ODB��
�ڡ�CAH�У���CHA=$\frac{180��-��C}{2}$��
��DMA=90��-$\frac{1}{2}$��C-��ODB��
�ߡ�CFD=180��-��C-2��ODB
��DMA=��AMO=90��-$\frac{1}{2}$��C-��ODB��
��$\frac{��AMO}{��DFC}$=$\frac{90��-\frac{1}{2}��C-��ODB}{180��-��C-2��ODB}$=$\frac{1}{2}$��
���� ������Ҫ�����˼��α任�ۺ��Լ�ż�η��Լ�����ֵ�����ʡ�����������������ε���ǵ�֪ʶ������Ӧ����������ǵ����ʵó��ǽ���ؼ���

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�| A�� | x2+2x-1=0 | B�� | x2-6x+9=0 | C�� | x2+4x+2=0 | D�� | -x2+x+2=0 |
| A�� | $\frac{3}{5}$ | B�� | 9 | C�� | 1 | D�� | ����ȷ�� |
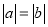 ����
����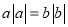 ������a2��5a+5=0����
������a2��5a+5=0����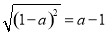 ����
����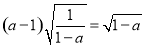
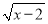 �������x��ȡֵ��Χ�ǣ�������
�������x��ȡֵ��Χ�ǣ�������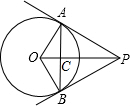 ��ͼ����PΪ��O��һ�㣬PA��PB�ֱ����O�������ڵ�A��B���߶�AB��OP�ཻ�ڵ�C������OA��OB����д����������Ϊ��ȷ�Ľ��ۣ�OA=OB���⣩��AP=BP����AOP�ա�BOP��
��ͼ����PΪ��O��һ�㣬PA��PB�ֱ����O�������ڵ�A��B���߶�AB��OP�ཻ�ڵ�C������OA��OB����д����������Ϊ��ȷ�Ľ��ۣ�OA=OB���⣩��AP=BP����AOP�ա�BOP��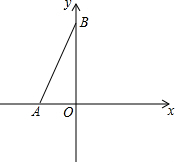 ��ͼ����ƽ��ֱ������ϵ�У�A��a��0����B��0��b������a��b����|a+b-4|+��2a+4��2=0��
��ͼ����ƽ��ֱ������ϵ�У�A��a��0����B��0��b������a��b����|a+b-4|+��2a+4��2=0��