题目内容
16.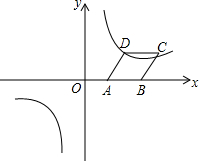 平面直角坐标系中,菱形ABCD的边AB在x轴上,已知点A(2,0),点C(10,4),双曲线经过点D.
平面直角坐标系中,菱形ABCD的边AB在x轴上,已知点A(2,0),点C(10,4),双曲线经过点D.(1)求菱形ABCD的边长;
(2)求双曲线的解析式.
分析 (1)过点C作CE⊥AB于点E,设菱形的边长为x,则BC=AB=x,BE=10-2-x,在Rt△BEC中,利用勾股定理建立关于x的方程,解方程求出x的值即可;
(2)设双曲线的解析式为y=$\frac{k}{x}$,过点D作DF⊥AB于点F,分别求出OF,DF的长,则点D的坐标可知,代入双曲线的解析式求出k的值即可.
解答 解:(1)设菱形的边长为x,则BC=AB=x,BE=10-2-x,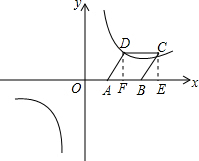
∵点C(10,4),
∴CE=4,
在Rt△BEC中,由勾股定理可得:BC2=BE2+CE2,
即x2=(10-2-x)2+42,
解得:x=5,
∴菱形ABCD的边长为5;
(2)设双曲线的解析式为y=$\frac{k}{x}$,过点D作DF⊥AB于点F,
∵DC∥AB,点C(10,4),
∴DF=4,
∵AB=5,
∴OF=OE-EF=10-5=5,
∴点D(5,4),
∴k=20,
∴$y=\frac{20}{x}$.
点评 本题考查了菱形的性质、勾股定理的运用、解一元二次方程以及利用待定系数法求双曲线的解析式,解题的关键是做高线,构造直角三角形,利用勾股定理求出菱形的边长.

练习册系列答案
相关题目
6. 如图所示是某几何体的三视图,则该几何体的侧面积是( )
如图所示是某几何体的三视图,则该几何体的侧面积是( )
 如图所示是某几何体的三视图,则该几何体的侧面积是( )
如图所示是某几何体的三视图,则该几何体的侧面积是( )| A. | $\sqrt{10}$π | B. | 2$\sqrt{10}$π | C. | 3π | D. | 6π |
4.若反比例函数的图象经过点(-2,3),则该反比例函数图象一定经过点( )
| A. | (2,-3) | B. | (-2,-3) | C. | (2,3) | D. | (-1,-6) |
 如图,EF∥BC,AC平分∠BAF,∠B=80°,则∠C=50°.
如图,EF∥BC,AC平分∠BAF,∠B=80°,则∠C=50°. 如图,在矩形ABCD中,DE⊥AC于点E,AB=12,AC=20,则cos∠ADE=$\frac{3}{5}$.
如图,在矩形ABCD中,DE⊥AC于点E,AB=12,AC=20,则cos∠ADE=$\frac{3}{5}$. 如图,在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0,$2\sqrt{3}}$).
如图,在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0,$2\sqrt{3}}$). 如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东46°,A、B两地同时开工,若干天后公路准确接通.
如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东46°,A、B两地同时开工,若干天后公路准确接通.