题目内容
1.已知x2+$\frac{1}{{x}^{2}}$-x-$\frac{1}{x}$=0,则x+$\frac{1}{x}$=$\frac{1±\sqrt{5}}{2}$.分析 设y=x+$\frac{1}{x}$,将原方程转化为关于y的一元二次方程,通过解该方程求得y的值,即x+$\frac{1}{x}$的值.
解答 解:由原方程,得
(x+$\frac{1}{x}$)2-(x+$\frac{1}{x}$)-1=0.
设y=x+$\frac{1}{x}$,则
y2-y-1=0,
y=$\frac{1±\sqrt{(-1)^{2}-4×1×(-1)}}{2}$=$\frac{1±\sqrt{5}}{2}$.即y=$\frac{1±\sqrt{5}}{2}$.
故答案是:$\frac{1±\sqrt{5}}{2}$.
点评 本题考查了换元法解分式方程.解题的关键是把x+$\frac{1}{x}$看成一个整体来计算,即换元法思想.

练习册系列答案
相关题目
12.一元二次方程2x2-3x-5=0的两个实数根分别为x1、x2,则x1+x2的值为( )
| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
6.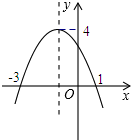 若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是( )
若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是( )
 若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是( )
若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是( )| A. | 0<k<4 | B. | -3<k<1 | C. | k<-3或k>1 | D. | k<4 |
11. 如图,直线AB,CD被直线EF所截,AB∥CD,∠1=110°,则∠2等于( )
如图,直线AB,CD被直线EF所截,AB∥CD,∠1=110°,则∠2等于( )
 如图,直线AB,CD被直线EF所截,AB∥CD,∠1=110°,则∠2等于( )
如图,直线AB,CD被直线EF所截,AB∥CD,∠1=110°,则∠2等于( )| A. | 90° | B. | 80° | C. | 70° | D. | 60° |
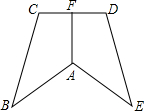 已知:如图,AB=AE,∠B=∠E,BC=ED,AF⊥CD,求证:CF=DF.
已知:如图,AB=AE,∠B=∠E,BC=ED,AF⊥CD,求证:CF=DF.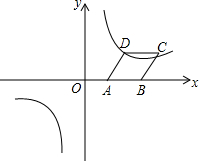 平面直角坐标系中,菱形ABCD的边AB在x轴上,已知点A(2,0),点C(10,4),双曲线经过点D.
平面直角坐标系中,菱形ABCD的边AB在x轴上,已知点A(2,0),点C(10,4),双曲线经过点D.