题目内容
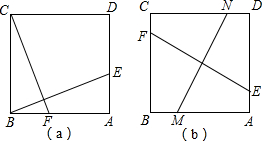 已知正方形ABCD,点E、F分别是AD、AB边上的点,且BE⊥CF;
已知正方形ABCD,点E、F分别是AD、AB边上的点,且BE⊥CF;(1)求证:CF=BE;
(2)如图(b),MN和EF是夹在正方形两组对边间的线段,且MN⊥EF,那么MN与EF相等吗?请简要说明你的判断思路,若需添加辅助线说明,请在(b)中画出.
考点:全等三角形的判定与性质,正方形的性质
专题:
分析:(1)根据正方形的性质,可得BA与BC的关系,根据同角的余角相等,可得∠BFC=∠AEB,根据全等三角形的判定与性质,可得答案;
(2)根据直角三角形的性质,可得∠1+∠4=90°,∠1与∠3的关系,根据AAS,可得三角形全等,根据全等三角形的性质,可得答案.
(2)根据直角三角形的性质,可得∠1+∠4=90°,∠1与∠3的关系,根据AAS,可得三角形全等,根据全等三角形的性质,可得答案.
解答:(1)证明:如图一:
 ,
,
∵四边形ABCD是正方形,
∴BC=BA,∠CBA=∠A=90°.
∵BE⊥CF,
∴∠BGF=90°,
∠GBF+∠GFB=90°.
∵∠FBG+∠BEA=90°,
∴∠BFC=∠AEB.
在△BFC和△AEB中,
,
∴△BFC≌△AEB(AAS),
∴CF=BE;
(2)如图二作MG⊥AB与G点,作EH⊥BC与H点,
∴∠NGM=∠NGA=90°,∠EHF=∠EHB=90°,
∴∠1+∠4=90°.
∴ADNG是矩形,AEHB是矩形,
∴AD=NG,AD∥NG,AB∥EH,AB=EH,
∴∠2=∠3.
∵MN⊥EF,
∴∠EIM=90°,
∴∠4+∠2=90°,
∠3+∠4=90°,
∴∠1=∠3.
正方形ABCD,
∴AD=AB,∠A=∠B=90°.
∴EH=NG.
在△EHF和△NGM中,
,
∴△EHF≌△△NGM (AAS),
∴EF=MN.
 ,
,∵四边形ABCD是正方形,
∴BC=BA,∠CBA=∠A=90°.
∵BE⊥CF,
∴∠BGF=90°,
∠GBF+∠GFB=90°.
∵∠FBG+∠BEA=90°,
∴∠BFC=∠AEB.
在△BFC和△AEB中,
|
∴△BFC≌△AEB(AAS),
∴CF=BE;
(2)如图二作MG⊥AB与G点,作EH⊥BC与H点,

∴∠NGM=∠NGA=90°,∠EHF=∠EHB=90°,
∴∠1+∠4=90°.
∴ADNG是矩形,AEHB是矩形,
∴AD=NG,AD∥NG,AB∥EH,AB=EH,
∴∠2=∠3.
∵MN⊥EF,
∴∠EIM=90°,
∴∠4+∠2=90°,
∠3+∠4=90°,
∴∠1=∠3.
正方形ABCD,
∴AD=AB,∠A=∠B=90°.
∴EH=NG.
在△EHF和△NGM中,
|
∴△EHF≌△△NGM (AAS),
∴EF=MN.
点评:本题考查了全等三角形的判定与性质,利用了正方形的性质,补角的性质,全等三角形的判定与性质,作图构造全等三角形是解题关键.

练习册系列答案
相关题目
方程
=1的解是( )
| 2 |
| x-3 |
| A、x=2 | B、x=3 |
| C、x=4 | D、x=5 |
如图,在矩形ABCD中,AB的长度为a,BC的长度为b,将此矩形纸片按下列顺序折叠,则
的是( )

| a |
| b |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在?ABCD中,E是BC的延长线上一点,AE与CD交于点F,BC=2CE.若AB=6,则DF的长为( )
如图,在?ABCD中,E是BC的延长线上一点,AE与CD交于点F,BC=2CE.若AB=6,则DF的长为( )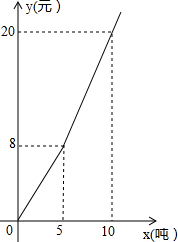 随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水.某市民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元).请根据图象信息,回答下列问题:
随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水.某市民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元).请根据图象信息,回答下列问题: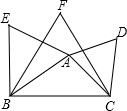 如图,根据图形解答下列问题
如图,根据图形解答下列问题 如图,在?ABCD中,AE∥CF,求证:AE=CF.
如图,在?ABCD中,AE∥CF,求证:AE=CF.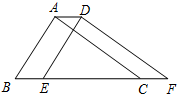 如图,将周长为8,面积为s的△ABC沿BC方向平移1个单位得到△DEF.
如图,将周长为8,面积为s的△ABC沿BC方向平移1个单位得到△DEF.