题目内容
已知函数y=-x+m与y=mx-4的图象的交点在x轴的负半轴上.
(1)求m的值;
(2)在同一直角坐标系内画出函数的图象;
(3)求两函数图象与y轴所围成的三角形的面积.
(1)求m的值;
(2)在同一直角坐标系内画出函数的图象;
(3)求两函数图象与y轴所围成的三角形的面积.
考点:两条直线相交或平行问题
专题:计算题
分析:(1)先表示出两函数图象与x轴的交点坐标,根据题意得到m=
,解得m=2或-2,由于交点在x轴的负半轴上,所以m=2;
(2)利用描点法画出两函数图象;
(3)先确定两直线与坐标轴的交点坐标,然后根据三角形面积公式求解.
| 4 |
| m |
(2)利用描点法画出两函数图象;
(3)先确定两直线与坐标轴的交点坐标,然后根据三角形面积公式求解.
解答:解:(1)∵函数y=-x+m与x轴的交点坐标为(m,0),函数y=mx-4与x轴的交点坐标为(
,0),
∴m=
,解得m1=2,m2=-2,
∵函数y=-x+m与y=mx-4的图象的交点在x轴的负半轴上,
∴m=-2;
(2)两函数解析式分别为y=-x-2,y=-2x-4,
函数图象为:
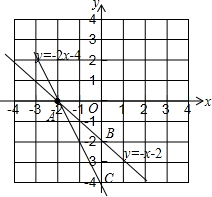
(3)如图,
∵A点坐标为(-2,0),B点坐标为(0,-2),C点坐标为(0,-4),
∴S△ABC=
×2×(-2+4)=2,
即两函数图象与y轴所围成的三角形的面积为2.
| 4 |
| m |
∴m=
| 4 |
| m |
∵函数y=-x+m与y=mx-4的图象的交点在x轴的负半轴上,
∴m=-2;
(2)两函数解析式分别为y=-x-2,y=-2x-4,
函数图象为:

(3)如图,
∵A点坐标为(-2,0),B点坐标为(0,-2),C点坐标为(0,-4),
∴S△ABC=
| 1 |
| 2 |
即两函数图象与y轴所围成的三角形的面积为2.
点评:本题考查了两条直线相交或平行问题:若直线y=k1x+b1与直线y=k2x+b2平行,则k1=k2;若直线y=k1x+b1与直线y=k2x+b2相交,则由两解析式所组成的方程组的解为交点坐标.

练习册系列答案
相关题目
 如图是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )
如图是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )A、 |
B、 |
C、 |
D、 |
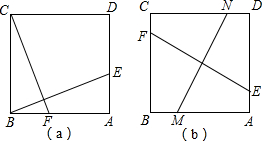 已知正方形ABCD,点E、F分别是AD、AB边上的点,且BE⊥CF;
已知正方形ABCD,点E、F分别是AD、AB边上的点,且BE⊥CF;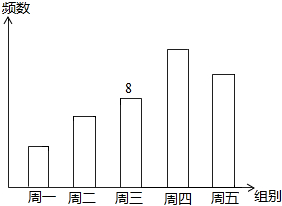 某校八年级一班进行为期5天的图案设计比赛,作品上交时限为周一至周五,班委会将参赛逐天进行统计,并绘制成如图所示的频数直方图.已知从左到右各矩形的高度比为2:3:4:6:5.且已知周三组的频数是8.
某校八年级一班进行为期5天的图案设计比赛,作品上交时限为周一至周五,班委会将参赛逐天进行统计,并绘制成如图所示的频数直方图.已知从左到右各矩形的高度比为2:3:4:6:5.且已知周三组的频数是8. 如图,在△ABC中,BD⊥AC,AB=6,AC=5
如图,在△ABC中,BD⊥AC,AB=6,AC=5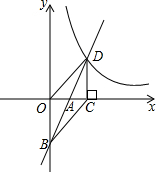 如图,在平面直角坐标系中,一次函数y=2x+b(b<0)的图象与坐标轴交于A、B两点,与函数y=
如图,在平面直角坐标系中,一次函数y=2x+b(b<0)的图象与坐标轴交于A、B两点,与函数y=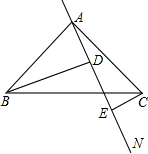 如图,已知在Rt△ABC中,AB=AC,∠BAC=90°,AN是过点A的任意一直线,BD⊥AN于点D,CE⊥AN于点E,则BD,CE,DE之间存在着怎样的关系?请说明理由.
如图,已知在Rt△ABC中,AB=AC,∠BAC=90°,AN是过点A的任意一直线,BD⊥AN于点D,CE⊥AN于点E,则BD,CE,DE之间存在着怎样的关系?请说明理由.