题目内容
如图,在矩形ABCD中,AB的长度为a,BC的长度为b,将此矩形纸片按下列顺序折叠,则
的是( )

| a |
| b |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:翻折变换(折叠问题)
专题:计算题
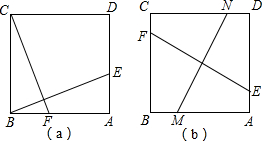
分析:由第一个图得到第二个图,根据折叠的性质得到BA=BF=a,∠BFE=∠A=90°,于是可判断四边形ABFE为正方形,则AE=AB=a,所以DE=CF=b-a,由第三个图得到EH=ED=b-a,由第四个图得到FH=FC=b-a,而EH+HF=EF=AB,所以b-a+b-a=a,再利用比例性质即可得到
=
.
| a |
| b |
| 2 |
| 3 |
解答:解:∵点A沿BE折叠到点F处,
∴BA=BF=a,∠BFE=∠A=90°,
∴四边形ABFE为正方形,
∴AE=AB=a,
∴DE=CF=b-a,
∵点D沿EG折叠到点H处,点C沿FG折叠到点H处,
∴EH=ED=b-a,FH=FC=b-a,
∵EH+HF=EF=AB,
∴b-a+b-a=a,即3a=2b,
∴
=
.
故选B.
∴BA=BF=a,∠BFE=∠A=90°,
∴四边形ABFE为正方形,
∴AE=AB=a,
∴DE=CF=b-a,
∵点D沿EG折叠到点H处,点C沿FG折叠到点H处,
∴EH=ED=b-a,FH=FC=b-a,
∵EH+HF=EF=AB,
∴b-a+b-a=a,即3a=2b,
∴
| a |
| b |
| 2 |
| 3 |
故选B.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
在平面直角坐标系中一点P(a,b)满足ab<0,a>b,则P点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )
如图是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )A、 |
B、 |
C、 |
D、 |
 如图,在∠1,∠2,∠3,∠4中,是内错角的是( )
如图,在∠1,∠2,∠3,∠4中,是内错角的是( )| A、∠1和∠2 |
| B、∠3和∠4 |
| C、∠2和∠3 |
| D、∠1和∠4 |
2014年1月30日晚,全国约有7.04亿人观看中央电视台播出的马年春节联欢晚会,7.04亿用科学记数法可表示为( )
| A、7.04×107 |
| B、7.04×108 |
| C、7.04×109 |
| D、7.04×1010 |
 已知正方形ABCD,点E、F分别是AD、AB边上的点,且BE⊥CF;
已知正方形ABCD,点E、F分别是AD、AB边上的点,且BE⊥CF;