题目内容
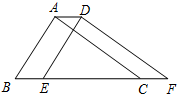 如图,将周长为8,面积为s的△ABC沿BC方向平移1个单位得到△DEF.
如图,将周长为8,面积为s的△ABC沿BC方向平移1个单位得到△DEF.(1)求四边形ABFD的周长;
(2)找出其中的平行四边形;
(3)若EC=5,求出其中平行四边形的面积.
考点:平行四边形的判定与性质,平移的性质
专题:
分析:(1)根据平移的性质和已知得出AD=CF=1,AB+BC+AC=8,DF=AC,即可求出答案;
(2)根据平移的性质和平行四边形的判定得出即可;
(3)求出平行四边形的高,即可求出答案.
(2)根据平移的性质和平行四边形的判定得出即可;
(3)求出平行四边形的高,即可求出答案.
解答:解:(1)∵将周长为8,面积为s的△ABC沿BC方向平移1个单位得到△DEF,
∴AD=CF=1,AB+BC+AC=8,DF=AC,
∴四边形ABFD的周长是AB+BC+CF+DF+AD=AB+BC+AC+1+1=8+2=10;
(2)平行四边形是四边形ABED和四边形ACFD;
(3)
过A作AN⊥BC于N,过D作DM⊥BC于M,
∵将周长为8,面积为s的△ABC沿BC方向平移1个单位得到△DEF,
∴AD∥BC,
∴AN=DM,
∵
×BC×AN=s,BC=1+5=6,
∴DM=AN=
s,
∴平行四边形ABED的面积是BE×AN=1×
s=
s,
同理平行四边形ACFD的面积是CF×DM=1×
s=
s.
∴AD=CF=1,AB+BC+AC=8,DF=AC,
∴四边形ABFD的周长是AB+BC+CF+DF+AD=AB+BC+AC+1+1=8+2=10;
(2)平行四边形是四边形ABED和四边形ACFD;
(3)

过A作AN⊥BC于N,过D作DM⊥BC于M,
∵将周长为8,面积为s的△ABC沿BC方向平移1个单位得到△DEF,
∴AD∥BC,
∴AN=DM,
∵
| 1 |
| 2 |
∴DM=AN=
| 1 |
| 3 |
∴平行四边形ABED的面积是BE×AN=1×
| 1 |
| 3 |
| 1 |
| 3 |
同理平行四边形ACFD的面积是CF×DM=1×
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查了平行四边形的判定和性质,平移的性质的应用,题目比较典型,难度不是很大.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
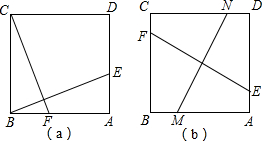 已知正方形ABCD,点E、F分别是AD、AB边上的点,且BE⊥CF;
已知正方形ABCD,点E、F分别是AD、AB边上的点,且BE⊥CF;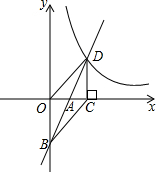 如图,在平面直角坐标系中,一次函数y=2x+b(b<0)的图象与坐标轴交于A、B两点,与函数y=
如图,在平面直角坐标系中,一次函数y=2x+b(b<0)的图象与坐标轴交于A、B两点,与函数y=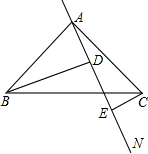 如图,已知在Rt△ABC中,AB=AC,∠BAC=90°,AN是过点A的任意一直线,BD⊥AN于点D,CE⊥AN于点E,则BD,CE,DE之间存在着怎样的关系?请说明理由.
如图,已知在Rt△ABC中,AB=AC,∠BAC=90°,AN是过点A的任意一直线,BD⊥AN于点D,CE⊥AN于点E,则BD,CE,DE之间存在着怎样的关系?请说明理由.