题目内容
 如图,矩形OABC在直角坐标系中,OA=4,OC=2,经过点P(-1,0)的直线将矩形OABC的面积两等分,则此直线的解析式为
如图,矩形OABC在直角坐标系中,OA=4,OC=2,经过点P(-1,0)的直线将矩形OABC的面积两等分,则此直线的解析式为考点:中心对称,待定系数法求一次函数解析式
专题:
分析:根据中心对称图形的性质得出矩形OABC的中心坐标,进而求出直线解析式.
解答:解:∵矩形OABC在直角坐标系中,OA=4,OC=2,
∴A(4,0),B(4,2),
故矩形OABC的中心坐标为:(2,1),
设经过点P(-1,0)的直线解析式为:y=ax+b,
则
,
解得:
,
故此直线的解析式为:y=
x+
.
故答案为:y=
x+
.
∴A(4,0),B(4,2),
故矩形OABC的中心坐标为:(2,1),
设经过点P(-1,0)的直线解析式为:y=ax+b,
则
|
解得:
|
故此直线的解析式为:y=
| 2 |
| 3 |
| 1 |
| 3 |
故答案为:y=
| 2 |
| 3 |
| 1 |
| 3 |
点评:此题主要考查了待定系数法求一次函数解析式以及中心对称图形的性质,得出其中点的坐标是解题关键.

练习册系列答案
相关题目
在Rt△ACB中,∠C=90°,sinB=
,则tanA=( )
| 1 |
| 5 |
A、
| ||||
B、
| ||||
C、2
| ||||
| D、24 |
 如图,∠COB=2∠AOC,OD平分∠AOB,∠AOB=114°,求∠COD的度数.
如图,∠COB=2∠AOC,OD平分∠AOB,∠AOB=114°,求∠COD的度数. 已知点D是△ABC的边AB上的中点,点E是AC上的一点,DF∥BE,EF∥AB,证明:AE、DF互相平分.
已知点D是△ABC的边AB上的中点,点E是AC上的一点,DF∥BE,EF∥AB,证明:AE、DF互相平分.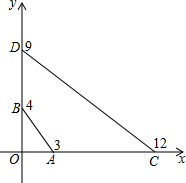 已知如图,A,B,C,D四点的坐标分别是(3,0),(0,4),(12,0),(0,9),探索∠OBA和∠OCD的大小关系,并说明理由.
已知如图,A,B,C,D四点的坐标分别是(3,0),(0,4),(12,0),(0,9),探索∠OBA和∠OCD的大小关系,并说明理由.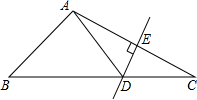 如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为12cm,求△ABC的周长.
如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为12cm,求△ABC的周长.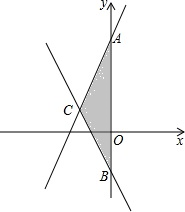 如图,已知直线y=2x+5和y=-x-1相交于点C,且两直线与y轴的交点分别是A,B.
如图,已知直线y=2x+5和y=-x-1相交于点C,且两直线与y轴的交点分别是A,B.