题目内容
在Rt△ACB中,∠C=90°,sinB=
,则tanA=( )
| 1 |
| 5 |
A、
| ||||
B、
| ||||
C、2
| ||||
| D、24 |
考点:互余两角三角函数的关系
专题:
分析:根据一个锐角的正弦等于它余角的余弦,可得cos∠A,再根据同角的正弦、余弦、正切的关系,可得答案.
解答:解:由在Rt△ACB中,∠C=90°,sinB=
,得
cos∠A=sinB=
,
sin∠A=
=
,
tan∠A=
=
=2
,
故选:C.
| 1 |
| 5 |
cos∠A=sinB=
| 1 |
| 5 |
sin∠A=
| 1-cos2∠A |
2
| ||
| 5 |
tan∠A=
| sin∠A |
| cos∠A |
| ||||
|
| 6 |
故选:C.
点评:本题考查了互为余角三角函数的关系,利用了一个锐角的正弦等于它余角的余弦,又利用了同角的正弦比余弦等于它的正切.

练习册系列答案
相关题目
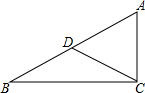 如图,∠ACB=90°,∠ADC=2∠B,AC=4,CD=3,求tan∠B.
如图,∠ACB=90°,∠ADC=2∠B,AC=4,CD=3,求tan∠B.
 将两个完全相同的长方形拼成如图的图形,长方形的长为a,宽为b,对角线长为c,请你用该图验证勾股定理.
将两个完全相同的长方形拼成如图的图形,长方形的长为a,宽为b,对角线长为c,请你用该图验证勾股定理. 如图,矩形OABC在直角坐标系中,OA=4,OC=2,经过点P(-1,0)的直线将矩形OABC的面积两等分,则此直线的解析式为
如图,矩形OABC在直角坐标系中,OA=4,OC=2,经过点P(-1,0)的直线将矩形OABC的面积两等分,则此直线的解析式为