题目内容
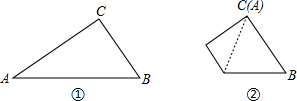 如图,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C重合(如图②);
如图,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C重合(如图②);(1)在图①中用尺规法作出折痕所在的直线l;(不写作法,保留痕迹)
(2)设直线l与AB、AC分别相交于点M、N,连结CM,若△CMB的周长是21cm,AB=14cm,求BC的长.
考点:翻折变换(折叠问题),作图—复杂作图
专题:
分析:(1)如图,分别以点A、点C为圆心,以大于
AC的长为半径画弧,过两弧的交点作直线即可解决问题.
(2)由题意得:AM=CM,进而得到BM+MC=AB=14,即可解决问题.
| 1 |
| 2 |
(2)由题意得:AM=CM,进而得到BM+MC=AB=14,即可解决问题.
解答: 解:(1)如图①,作图痕迹为相交的弧线.
解:(1)如图①,作图痕迹为相交的弧线.
(2)由题意得:AM=CM,
∴BM+MC=BM+AM=AB=14,
∵△CMB的周长是21,
∴BC=21-14=7(cm).
 解:(1)如图①,作图痕迹为相交的弧线.
解:(1)如图①,作图痕迹为相交的弧线.(2)由题意得:AM=CM,
∴BM+MC=BM+AM=AB=14,
∵△CMB的周长是21,
∴BC=21-14=7(cm).
点评:该题主要考查了翻折变换的性质及其应用问题;根据翻折变换的性质准确找出图形中隐含的数量关系是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
据相关媒体报道,2015年国家有望将房屋不动产纳入税务抵扣范围,此项改革或伴随房地产、建筑业“营改增”同步进行.分析称此项改革或带来超过8000亿元的减税规模,可进一步鼓励和刺激投资,房地产价格也可能因此调整.请用科学记数法表示出此项改革或带来超过多少元的减税规模( )
| A、8.0×1011 |
| B、8.0×1010 |
| C、8.0×106 |
| D、8.0×103 |
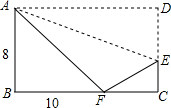 如图,在平面直角坐标系中放入一张长方形纸片ABCD,其中B是坐标原点,BC,AB分别在x轴、y轴的正半轴上,现将纸片沿AE翻折,使点D落在x轴上,记为F,若AB=8,BC=10,则E点的坐标为( )
如图,在平面直角坐标系中放入一张长方形纸片ABCD,其中B是坐标原点,BC,AB分别在x轴、y轴的正半轴上,现将纸片沿AE翻折,使点D落在x轴上,记为F,若AB=8,BC=10,则E点的坐标为( )| A、(10,4) |
| B、(10,3) |
| C、(6,4) |
| D、(6,3) |
 函数y=x2+bx+c与y=x的图象如图所示,下面结论:①b2-4c>0,②b+c+1=0,③3b+c+6=0,④当1<x<3时,x2+(b-1)x+c<0,其中正确的是( )
函数y=x2+bx+c与y=x的图象如图所示,下面结论:①b2-4c>0,②b+c+1=0,③3b+c+6=0,④当1<x<3时,x2+(b-1)x+c<0,其中正确的是( )
 如图,AB∥CD,OB⊥AB,∠D=120°,则∠O=
如图,AB∥CD,OB⊥AB,∠D=120°,则∠O= 如图所示,OB,OC分别平分∠ABC,∠ACB,且∠BOC=128°,则∠A=
如图所示,OB,OC分别平分∠ABC,∠ACB,且∠BOC=128°,则∠A=