题目内容
5.①${(\frac{1}{2})^{-1}}-\sqrt{{{(-3)}^2}}+(π-3.14){\;}^0-\sqrt{2}cos45$°②解方程:$\frac{x}{x-2}+\frac{4}{2-x}=-1$.
分析 ①原式利用零指数幂、负整数指数幂法则,二次根式性质,以及特殊角的三角函数值计算即可得到结果;
②分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:①原式=2-3+1-1=-1;
②去分母得:x-4=-x+2,
移项合并得:2x=6,
解得:x=3,
检验:当x=3时,x-2=1≠0,
则x=3是原方程的解.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列几何图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 菱形 | D. | 正五边形 |
 如图是由5个相同的正方体组成的一个立体图形,它的左视图是( )
如图是由5个相同的正方体组成的一个立体图形,它的左视图是( )



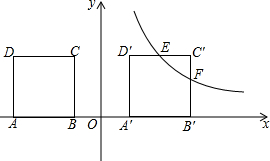 如图,在平面直角坐标系中,正方形ABCD顶点D(-3,2),B(1,0),CD∥x轴,将正方形ABCD向右平移m个单位,得正方形A′B′C′D′.当 m=4时,反比例函数y=$\frac{k}{x}$(x>0)的图象过线段C′D′的中点E,与线段B′C′交于点F.
如图,在平面直角坐标系中,正方形ABCD顶点D(-3,2),B(1,0),CD∥x轴,将正方形ABCD向右平移m个单位,得正方形A′B′C′D′.当 m=4时,反比例函数y=$\frac{k}{x}$(x>0)的图象过线段C′D′的中点E,与线段B′C′交于点F.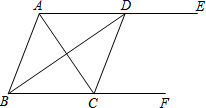 如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.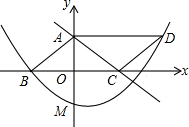 如图,平行四边形ABCD中,D点在抛物线y=$\frac{1}{8}$x2+bx+c上,且OB=OC,AB=5,tan∠ACB=$\frac{3}{4}$,M是抛物线与y轴的交点.
如图,平行四边形ABCD中,D点在抛物线y=$\frac{1}{8}$x2+bx+c上,且OB=OC,AB=5,tan∠ACB=$\frac{3}{4}$,M是抛物线与y轴的交点.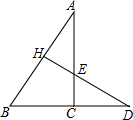 如图所示,DH⊥AB于H,AC⊥BD于C,DH与AC相交于点E,仔细观察图形,回答以下问题:
如图所示,DH⊥AB于H,AC⊥BD于C,DH与AC相交于点E,仔细观察图形,回答以下问题: