题目内容
8.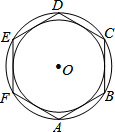 如图,正六边形ABCDEF的边长为2,则该正六边形的外接圆与内切圆所形成的圆环面积为π.
如图,正六边形ABCDEF的边长为2,则该正六边形的外接圆与内切圆所形成的圆环面积为π.
分析 连接OA、OB,作OM⊥AB于M,证明△AOB是等边三角形,得出OA=AB=2,AM=$\frac{1}{2}$AB=1,由勾股定理求出OM,再由圆的面积公式即可得出圆环的面积.
解答 解:连接OA、OB,作OM⊥AB于M,如图所示: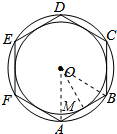
则∠AOB=$\frac{360°}{6}$=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴OA=AB=2,AM=$\frac{1}{2}$AB=1,
∴OM=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
即正六边形外接圆的半径=2,
它的内切圆的半径=$\sqrt{3}$,
所以圆环的面积=π[22-($\sqrt{3}$)2]=π;
故答案为:π.
点评 本题考查了正六边形的性质、等边三角形的判定与性质、勾股定理;由正六边形的性质得出正六边形的边长与它的外接圆的半径的关系和与内切圆的半径的关系是解决问题的关键.

练习册系列答案
相关题目
18.下列四个实数最小的是( )
| A. | -1 | B. | -$\sqrt{2}$ | C. | 0 | D. | 1 |
19. 如图,将矩形ABCD纸片沿EF折叠,若∠BGE=130°,则∠GEF等于( )
如图,将矩形ABCD纸片沿EF折叠,若∠BGE=130°,则∠GEF等于( )
 如图,将矩形ABCD纸片沿EF折叠,若∠BGE=130°,则∠GEF等于( )
如图,将矩形ABCD纸片沿EF折叠,若∠BGE=130°,则∠GEF等于( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |

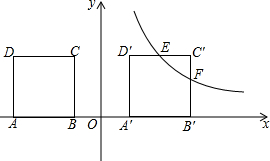 如图,在平面直角坐标系中,正方形ABCD顶点D(-3,2),B(1,0),CD∥x轴,将正方形ABCD向右平移m个单位,得正方形A′B′C′D′.当 m=4时,反比例函数y=$\frac{k}{x}$(x>0)的图象过线段C′D′的中点E,与线段B′C′交于点F.
如图,在平面直角坐标系中,正方形ABCD顶点D(-3,2),B(1,0),CD∥x轴,将正方形ABCD向右平移m个单位,得正方形A′B′C′D′.当 m=4时,反比例函数y=$\frac{k}{x}$(x>0)的图象过线段C′D′的中点E,与线段B′C′交于点F.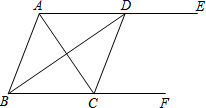 如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.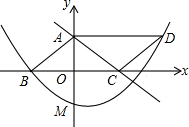 如图,平行四边形ABCD中,D点在抛物线y=$\frac{1}{8}$x2+bx+c上,且OB=OC,AB=5,tan∠ACB=$\frac{3}{4}$,M是抛物线与y轴的交点.
如图,平行四边形ABCD中,D点在抛物线y=$\frac{1}{8}$x2+bx+c上,且OB=OC,AB=5,tan∠ACB=$\frac{3}{4}$,M是抛物线与y轴的交点.