题目内容
10.抛物线y=x2-4x+3的顶点坐标是(2,-1).分析 根据抛物线y=x2-4x+3,可以将此函数的解析式化为顶点式,从而可以得到它的顶点坐标,本题得以解决.
解答 解:∵y=x2-4x+3=(x-2)2-1,
∴抛物线y=x2-4x+3的顶点坐标是(2,-1),
故答案是:(2,-1).
点评 本题考查二次函数的性质,解题的关键是会将二次函数的一般式化为顶点式.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
1.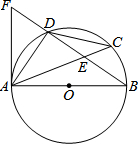 如图,AB是⊙O的直径,D是$\widehat{AC}$的中点,弦AC与弦BD交于点E,点F在BD的延长线上,且DF=DE.
如图,AB是⊙O的直径,D是$\widehat{AC}$的中点,弦AC与弦BD交于点E,点F在BD的延长线上,且DF=DE.
(1)求证:AF是⊙O的切线;
(2)若AD=5,AC=8,求⊙O的半径.
 如图,AB是⊙O的直径,D是$\widehat{AC}$的中点,弦AC与弦BD交于点E,点F在BD的延长线上,且DF=DE.
如图,AB是⊙O的直径,D是$\widehat{AC}$的中点,弦AC与弦BD交于点E,点F在BD的延长线上,且DF=DE.(1)求证:AF是⊙O的切线;
(2)若AD=5,AC=8,求⊙O的半径.
1.已知关于x的方程x2-kx-4=0的一个根为x=3,则实数k的值为( )
| A. | 5 | B. | 3 | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
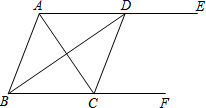 如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.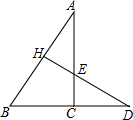 如图所示,DH⊥AB于H,AC⊥BD于C,DH与AC相交于点E,仔细观察图形,回答以下问题:
如图所示,DH⊥AB于H,AC⊥BD于C,DH与AC相交于点E,仔细观察图形,回答以下问题: