题目内容
在平面直角坐标系中,抛物线y=x2+(k-1)x-k与直线y=kx+1交于A,B两点,点A在点B的左侧.
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k-1)x-k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
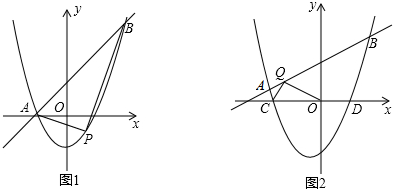
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k-1)x-k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
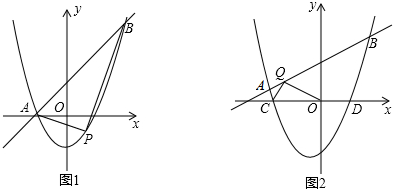
考点:二次函数综合题
专题:代数几何综合题,压轴题
分析:(1)当k=1时,联立抛物线与直线的解析式,解方程求得点A、B的坐标;
(2)如答图2,作辅助线,求出△ABP面积的表达式,然后利用二次函数的性质求出最大值及点P的坐标;
(3)“存在唯一一点Q,使得∠OQC=90°”的含义是,以OC为直径的圆与直线AB相切于点Q,由圆周角定理可知,此时∠OQC=90°且点Q为唯一.以此为基础,构造相似三角形,利用比例式列出方程,求得k的值.需要另外注意一点是考虑直线AB是否与双曲线交于C点,此时亦存在唯一一点Q,使得∠OQC=90°.
(2)如答图2,作辅助线,求出△ABP面积的表达式,然后利用二次函数的性质求出最大值及点P的坐标;
(3)“存在唯一一点Q,使得∠OQC=90°”的含义是,以OC为直径的圆与直线AB相切于点Q,由圆周角定理可知,此时∠OQC=90°且点Q为唯一.以此为基础,构造相似三角形,利用比例式列出方程,求得k的值.需要另外注意一点是考虑直线AB是否与双曲线交于C点,此时亦存在唯一一点Q,使得∠OQC=90°.
解答:解:(1)当k=1时,抛物线解析式为y=x2-1,直线解析式为y=x+1.
联立两个解析式,得:x2-1=x+1,
解得:x=-1或x=2,
当x=-1时,y=x+1=0;当x=2时,y=x+1=3,
∴A(-1,0),B(2,3).
(2)设P(x,x2-1).
如答图2所示,过点P作PF∥y轴,交直线AB于点F,则F(x,x+1).

∴PF=yF-yP=(x+1)-(x2-1)=-x2+x+2.
S△ABP=S△PFA+S△PFB=
PF(xF-xA)+
PF(xB-xF)=
PF(xB-xA)=
PF
∴S△ABP=
(-x2+x+2)=-
(x-
)2+
当x=
时,yP=x2-1=-
.
∴△ABP面积最大值为
,此时点P坐标为(
,-
).
(3)设直线AB:y=kx+1与x轴、y轴分别交于点E、F,
则E(-
,0),F(0,1),OE=
,OF=1.
在Rt△EOF中,由勾股定理得:EF=
=
.
令y=x2+(k-1)x-k=0,即(x+k)(x-1)=0,解得:x=-k或x=1.
∴C(-k,0),OC=k.
Ⅰ、假设存在唯一一点Q,使得∠OQC=90°,如答图3所示,
则以OC为直径的圆与直线AB相切于点Q,根据圆周角定理,此时∠OQC=90°.

设点N为OC中点,连接NQ,则NQ⊥EF,NQ=CN=ON=
.
∴EN=OE-ON=
-
.
∵∠NEQ=∠FEO,∠EQN=∠EOF=90°,
∴△EQN∽△EOF,
∴
=
,即:
=
,
解得:k=±
,
∵k>0,
∴k=
.
∴存在唯一一点Q,使得∠OQC=90°,此时k=
.
Ⅱ、若直线AB过点C时,此时直线与圆的交点只有另一点Q点,故亦存在唯一一点Q,使得∠OQC=90°,
将C(-k,0)代入y=kx+1中,
可得k=1,k=-1(舍去),
故存在唯一一点Q,使得∠OQC=90°,此时k=1.
综上所述,k=
或1时,存在唯一一点Q,使得∠OQC=90°.
联立两个解析式,得:x2-1=x+1,
解得:x=-1或x=2,
当x=-1时,y=x+1=0;当x=2时,y=x+1=3,
∴A(-1,0),B(2,3).
(2)设P(x,x2-1).
如答图2所示,过点P作PF∥y轴,交直线AB于点F,则F(x,x+1).

∴PF=yF-yP=(x+1)-(x2-1)=-x2+x+2.
S△ABP=S△PFA+S△PFB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴S△ABP=
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 27 |
| 8 |
当x=
| 1 |
| 2 |
| 3 |
| 4 |
∴△ABP面积最大值为
| 27 |
| 8 |
| 1 |
| 2 |
| 3 |
| 4 |
(3)设直线AB:y=kx+1与x轴、y轴分别交于点E、F,
则E(-
| 1 |
| k |
| 1 |
| k |
在Rt△EOF中,由勾股定理得:EF=
(
|
| ||
| k |
令y=x2+(k-1)x-k=0,即(x+k)(x-1)=0,解得:x=-k或x=1.
∴C(-k,0),OC=k.
Ⅰ、假设存在唯一一点Q,使得∠OQC=90°,如答图3所示,
则以OC为直径的圆与直线AB相切于点Q,根据圆周角定理,此时∠OQC=90°.

设点N为OC中点,连接NQ,则NQ⊥EF,NQ=CN=ON=
| k |
| 2 |
∴EN=OE-ON=
| 1 |
| k |
| k |
| 2 |
∵∠NEQ=∠FEO,∠EQN=∠EOF=90°,
∴△EQN∽△EOF,
∴
| NQ |
| OF |
| EN |
| EF |
| ||
| 1 |
| ||||
|
解得:k=±
2
| ||
| 5 |
∵k>0,
∴k=
2
| ||
| 5 |
∴存在唯一一点Q,使得∠OQC=90°,此时k=
2
| ||
| 5 |
Ⅱ、若直线AB过点C时,此时直线与圆的交点只有另一点Q点,故亦存在唯一一点Q,使得∠OQC=90°,
将C(-k,0)代入y=kx+1中,
可得k=1,k=-1(舍去),
故存在唯一一点Q,使得∠OQC=90°,此时k=1.
综上所述,k=
2
| ||
| 5 |
点评:本题是二次函数压轴题,综合考查了二次函数及一次函数的图象与性质、解方程、勾股定理、直线与圆的位置关系、相似等重要知识点,有一定的难度.第(2)问中,注意图形面积的计算方法;第(3)问中,解题关键是理解“存在唯一一点Q,使得∠OQC=90°”的含义.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
在平面直角坐标系中,已知点A的坐标是(2,3),点B的坐标是(1,0),点C是点A关于点B的对称点,则点C的坐标是( )
| A、(2,-3) |
| B、(-2,-3) |
| C、(0,-2) |
| D、(0,-3) |

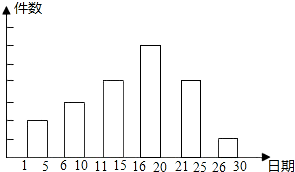 学校举办一项小制作评比活动.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的作品件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的件数是12.
学校举办一项小制作评比活动.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的作品件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的件数是12. 如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形.
如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形. 马航MH370航班于2014年3月8日凌晨与地面失去了联系,至今尚未找到有关马航MH370的任何消息.我国在第一时间派出了飞机和船只进行寻找.如图,某日在马航MH370失联的附近海域有两艘自西向东航行的海监船A、B正在执行搜索任务,B船在A船的正东方向,且两船保持20海里的距离,某一时刻在海监船A的东北方向,B的北偏东15°方向的我国渔政执法船C侦测到了疑似物品,上级命令B船马上前去支援,已知B船的速度是30海里/小时,求B船到达C船的时间是多少.(结果保留根号)
马航MH370航班于2014年3月8日凌晨与地面失去了联系,至今尚未找到有关马航MH370的任何消息.我国在第一时间派出了飞机和船只进行寻找.如图,某日在马航MH370失联的附近海域有两艘自西向东航行的海监船A、B正在执行搜索任务,B船在A船的正东方向,且两船保持20海里的距离,某一时刻在海监船A的东北方向,B的北偏东15°方向的我国渔政执法船C侦测到了疑似物品,上级命令B船马上前去支援,已知B船的速度是30海里/小时,求B船到达C船的时间是多少.(结果保留根号)