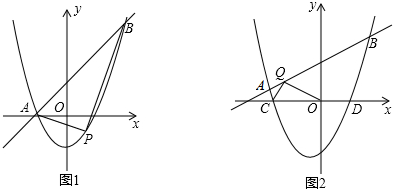题目内容
如图,在平面直角坐标系xOy中,△OAB如图放置,点A的坐标为(3,4),点P是AB边上的一点,过点P的反比例函数y=
(k>0,x>0)与OA边交于点E,连接OP.
(1)如图1,若点B的坐标为(5,0),且△OPB的面积为
,求反比例函数的解析式;
(2)如图2,过P作PC∥OA,与OB交于点C,若PC=
OE,并且△OPC的面积为
,求OE的长.

| k |
| x |
(1)如图1,若点B的坐标为(5,0),且△OPB的面积为
| 5 |
| 2 |
(2)如图2,过P作PC∥OA,与OB交于点C,若PC=
| 1 |
| 2 |
| 3 |
| 2 |

考点:反比例函数综合题
专题:
分析:(1)过点P作PD⊥OB于点D,根据点B的坐标为(5,0),且△OPB的面积为
求出PD的长,求出直线AB的解析式,故可得出P点坐标,利用待定系数法求出反比例函数的解析式即可;
(2)先根据勾股定理求出OA的长,△OPC的面积为
求出OC的长,再由PC∥OA可知△BCP∽△BOA,故可得出OC的长,由PC=
OE即可得出OE的长.
| 5 |
| 2 |
(2)先根据勾股定理求出OA的长,△OPC的面积为
| 3 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)过点P作PD⊥OB于点D,
解:(1)过点P作PD⊥OB于点D,
∵点B的坐标为(5,0),
△OPB的面积为
,
∴
×5PD=
,解得PD=1,
设直线AB的解析式为
y=ax+b(a≠0),
∵A(3,4),B(5,0),
∴
,解得
,
∴直线AB的解析式为y=-2x+10,
当y=1时,-2x+10=1,解得x=
,
∴P(
,1),
∵点P的反比例函数y=
(x>0)上,
∴1=
,解得k=
,
∴反比例函数的解析式为:y=
;
(2)∵点A的坐标为(3,4),
∴OA=
=5,
∵△OPC的面积为
,
∴
OC×1=
,解得OC=3,
∴BC=5-3=2,
∵PC∥OA,
∴△BCP∽△BOA,
∴
=
,即
=
,解得PC=2,
∵PC=
OE,
∴OE=4.
 解:(1)过点P作PD⊥OB于点D,
解:(1)过点P作PD⊥OB于点D,∵点B的坐标为(5,0),
△OPB的面积为
| 5 |
| 2 |
∴
| 1 |
| 2 |
| 5 |
| 2 |
设直线AB的解析式为
y=ax+b(a≠0),
∵A(3,4),B(5,0),
∴
|
|
∴直线AB的解析式为y=-2x+10,
当y=1时,-2x+10=1,解得x=
| 9 |
| 2 |
∴P(
| 9 |
| 2 |
∵点P的反比例函数y=
| k |
| x |
∴1=
| k | ||
|
| 9 |
| 2 |
∴反比例函数的解析式为:y=
| 9 |
| 2x |
(2)∵点A的坐标为(3,4),
∴OA=
| 32+42 |
∵△OPC的面积为
| 3 |
| 2 |
∴
| 1 |
| 2 |
| 3 |
| 2 |
∴BC=5-3=2,
∵PC∥OA,
∴△BCP∽△BOA,
∴
| PC |
| OA |
| BC |
| OB |
| PC |
| 5 |
| 2 |
| 5 |
∵PC=
| 1 |
| 2 |
∴OE=4.
点评:本题考查的是反比例函数综合题,涉及到用待定系数法求一次函数及反比例函数的解析式、相似三角形的判定与性质等知识,难度适中.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 实数a、b在数轴上的位置如图,且点(a,b)在一次函数y=2x+4图象上,则代数式
实数a、b在数轴上的位置如图,且点(a,b)在一次函数y=2x+4图象上,则代数式
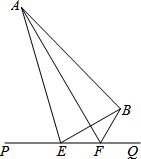 如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.