题目内容
18.如果x≥1,那么化简$\sqrt{-(1-x)^{3}}$的结果是(x-1)$\sqrt{x-1}$.分析 根据二次根式有意义的条件即可求出答案
解答 解:∵x≥1,
∴1-x≤0,
∴-(1-x)≥0,
∴原式=$\sqrt{-(1-x)^{2}(1-x)}$
=|1-x|$\sqrt{-(1-x)}$
=(x-1)$\sqrt{-(1-x)}$
=(x-1)$\sqrt{x-1}$
故答案为:(x-1)$\sqrt{x-1}$
点评 本题考查二次根式的性质与化简,解题的关键是熟练运用二次根式的性质,本题属于基础题型.

练习册系列答案
相关题目
3.在平面直角坐标系中,点(m2+1,1)一定在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.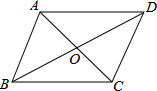 如图,要使平行四边形ABCD是矩形,可添加的条件是( )
如图,要使平行四边形ABCD是矩形,可添加的条件是( )
 如图,要使平行四边形ABCD是矩形,可添加的条件是( )
如图,要使平行四边形ABCD是矩形,可添加的条件是( )| A. | OA=OC OB=OD | B. | AC=BD | C. | AB=BC | D. | AC⊥BD |

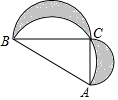 如图,Rt△ABC中,∠C=90°,AC=4,BC=9,分别以它的三边为直径向上作三个半圆,则图中阴影部分面积为18-$\frac{47}{8}$π.
如图,Rt△ABC中,∠C=90°,AC=4,BC=9,分别以它的三边为直径向上作三个半圆,则图中阴影部分面积为18-$\frac{47}{8}$π.