题目内容
6.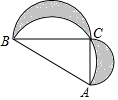 如图,Rt△ABC中,∠C=90°,AC=4,BC=9,分别以它的三边为直径向上作三个半圆,则图中阴影部分面积为18-$\frac{47}{8}$π.
如图,Rt△ABC中,∠C=90°,AC=4,BC=9,分别以它的三边为直径向上作三个半圆,则图中阴影部分面积为18-$\frac{47}{8}$π.
分析 根据勾股定理求出AB的长,即可用减法求出阴影部分的面积.
解答 解:由勾股定理AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{9}^{2}+{4}^{2}}$=$\sqrt{97}$.
根据题意得:S阴影=$\frac{1}{2}$π×($\frac{4}{2}$)2+$\frac{1}{2}$π×($\frac{9}{2}$)2+$\frac{1}{2}$×4×9-$\frac{1}{2}$π×($\frac{\sqrt{97}}{2}$)2=18-$\frac{47}{8}$π.
故答案是:18-$\frac{47}{8}$π.
点评 本题考查了扇形的面积计算,勾股定理.观察图形的特点,用各面积相加减,可得出阴影部分的面积.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
11.下列说法正确的是( )
| A. | 对角线相等的四边形是平行四边形 | |
| B. | 对角线互相平分的四边形是平行四边形 | |
| C. | 对角线互相垂直的四边形是平行四边形 | |
| D. | 对角线互相垂直且相等的四边形是平行四边形 |
16. 如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠2=42°,则∠1的度数是( )
如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠2=42°,则∠1的度数是( )
 如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠2=42°,则∠1的度数是( )
如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠2=42°,则∠1的度数是( )| A. | 38° | B. | 42° | C. | 48° | D. | 58° |
 如图,在平行四边形ABCD中,E为AD上一点,∠EBC=40°,且BE=BC,CE=CD,则∠A=110°.
如图,在平行四边形ABCD中,E为AD上一点,∠EBC=40°,且BE=BC,CE=CD,则∠A=110°. 如图,AB是⊙O的直径,点C为AB上面半圆上一点,点D为AB的下面半圆的中点,连接CD与AB交于点E,延长BA至F,使EF=CF.
如图,AB是⊙O的直径,点C为AB上面半圆上一点,点D为AB的下面半圆的中点,连接CD与AB交于点E,延长BA至F,使EF=CF. 在如图所示的长方体中,AB=2,BC=2,高CG=4.则从点A到点G的最短路线长为4$\sqrt{2}$.
在如图所示的长方体中,AB=2,BC=2,高CG=4.则从点A到点G的最短路线长为4$\sqrt{2}$.