题目内容
9.已知四边形ABCD为矩形,∠DAB的角平分线交直线CD于点E,若CE=2,AB=5,则AD的长为3或7.分析 根据矩形的性质和角平分线的性质证得△ADE是等腰直角三角形,当E在线段DC上时,AD=DE=DC-CE,当E在线段DC延长线上时AD=DE=DC+CE,代入数值即可求得答案.
解答 解:①当E在线段DC上时, 如图1,
如图1,
∵四边形ABCD为矩形,
∴∠BAD=∠D=90°,CD=AB=5,
∵AE平分∠DAB,
∴∠DAE=45°,
∴∠AED=45°,
∴∠DAE=∠AED,
∴AD=DE=DC-CE=5-2=3;
②当E在线段DC延长线上时,如图2,
∵四边形ABCD为矩形,
∴∠BAD=∠D=90°,CD=AB=5,
∵AE平分∠DAB,
∴∠DAE=45°,
∴∠AED=45°,
∴∠DAE=∠AED,
∴AD=DE=DC+CE=5+2=7,
综上:AD的长为3或7,
故答案为:3或7.
点评 本题主要考查了矩形的性质,等腰直角三角形的性质和判定,能够正确分类是解题的关键.

练习册系列答案
相关题目
19.如图,下列四个天平中,相同形状的物体的重量是相等的,其中第①个天平是平衡的,根据第①个天平,后三个天平中不平衡的有( )


| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
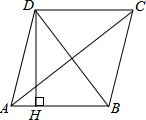 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,试求DH的长.
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,试求DH的长.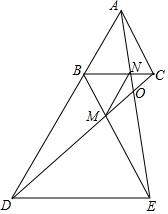 如图,点B在AD上,△ABC和△BDE是等边三角形,CD交BE于点M,AE交BC,CD于点N,O,连接MN.
如图,点B在AD上,△ABC和△BDE是等边三角形,CD交BE于点M,AE交BC,CD于点N,O,连接MN. 如图,AB是⊙O的直径,点C为AB上面半圆上一点,点D为AB的下面半圆的中点,连接CD与AB交于点E,延长BA至F,使EF=CF.
如图,AB是⊙O的直径,点C为AB上面半圆上一点,点D为AB的下面半圆的中点,连接CD与AB交于点E,延长BA至F,使EF=CF.