题目内容
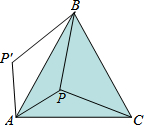 如图,P是正三角形ABC内一点,PA=5,PB=12,PC=13,若三角形PAC绕点A逆时针旋转后,得到三角形P′AB,则∠APB=
如图,P是正三角形ABC内一点,PA=5,PB=12,PC=13,若三角形PAC绕点A逆时针旋转后,得到三角形P′AB,则∠APB=考点:旋转的性质,等边三角形的判定与性质,勾股定理的逆定理
专题:计算题
分析:连结PP′,如图,利用等边三角形的性质得AB=AC,∠BAC=60°,再根据旋转的性质得∠PAP′=∠CAB=60°,AP=AP′=5,PC=P′B=13,则可判断△APP′为等边三角形,得到∠APP′=60°,PP′=AP=5,在△BPP′中运用勾股定理的逆定理可证明△BPP′为直角三角形,∠BPP′=90°,然后根据∠APB=∠APP′+∠BPP′进行计算即可.
解答:解:连结PP′,如图,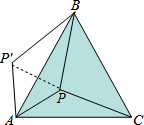
∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴∠PAP′=∠CAB=60°,AP=AP′=5,PC=P′B=13,
∴△APP′为等边三角形,
∴∠APP′=60°,PP′=AP=5,
在△BPP′中,∵PP′=5,P′B=13,BP=12,
∴BP2+PP′2=BP′2,
∴△BPP′为直角三角形,∠BPP′=90°,
∴∠APB=∠APP′+∠BPP′=60°+90°=150°.
故答案为150°.

∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴∠PAP′=∠CAB=60°,AP=AP′=5,PC=P′B=13,
∴△APP′为等边三角形,
∴∠APP′=60°,PP′=AP=5,
在△BPP′中,∵PP′=5,P′B=13,BP=12,
∴BP2+PP′2=BP′2,
∴△BPP′为直角三角形,∠BPP′=90°,
∴∠APB=∠APP′+∠BPP′=60°+90°=150°.
故答案为150°.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角.旋转前、后的图形全等.灵活应用等边三角形的判定与性质和勾股定理的逆定理.

练习册系列答案
相关题目
 用反证法证明命题:“如图,如果AB∥CD,AB∥EF,那么CD∥EF”,证明的第一个步骤是( )
用反证法证明命题:“如图,如果AB∥CD,AB∥EF,那么CD∥EF”,证明的第一个步骤是( )| A、假定CD∥EF |
| B、已知AB∥EF |
| C、假定CD不平行于EF |
| D、假定AB不平行于EF |

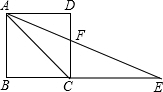 如图,点E在正方形ABCD的边BC的延长线上,且CE=CA,AE与CD交于F点,DF=
如图,点E在正方形ABCD的边BC的延长线上,且CE=CA,AE与CD交于F点,DF=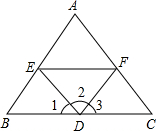 如图,请完成下列各题:
如图,请完成下列各题: