题目内容
(1)如图1,在△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足为E,试探究线段BE和CD之间的数量关系,并写出你的理由.
(2)如图2,把条件改为:“在△ABC中,AB=AC,∠BAC=90°,点D在BC上,∠EDB=
∠C,BE⊥ED,DE与AB相交于F点,则线段BE和FD之间的数量关系如何?并证明你的结论.”

(2)如图2,把条件改为:“在△ABC中,AB=AC,∠BAC=90°,点D在BC上,∠EDB=
| 1 |
| 2 |

考点:全等三角形的判定与性质
专题:
分析:(1)如图,作辅助线;证明△ADC≌△AFB,得到DC=BF;证明EF=BE,即可解决问题.
(2)如图,作辅助线;△HFD≌△HGB,得到DF=BG;证明△EGD≌△EBD,得到BE=GE,即可解决问题.
(2)如图,作辅助线;△HFD≌△HGB,得到DF=BG;证明△EGD≌△EBD,得到BE=GE,即可解决问题.
解答: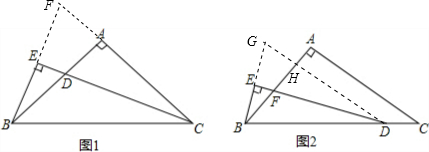 解:CD=2BE;理由如下:如图1,∵∠BAC=90°,
解:CD=2BE;理由如下:如图1,∵∠BAC=90°,
∠E=90°,
∴∠FED+∠FAD=180°,
∴A、F、E、D四点共圆,
∴∠ADC=∠F;在△ADC与△AFB中,
,
∴△ADC≌△AFB(AAS),
∴DC=BF;
在△EFC与△EBC中,
,
∴△EFC≌△EBC(ASA),
∴EF=BE,
∴CD=2BE.
(2)DF=2BE.理由如下:
如图,作DG∥AC,交BE的延长线于点G;
则∠BDG=∠C;
∵∠EDB=
∠C,
∴DE平分∠BDG;
∵DG∥AC,
∴∠BHD=∠A=90°,
而∠HBD=45°,故∠HDB=45°,
∴BH=DH;
∵∠GEF+∠GHF=180°,
∴G、E、F、H四点共圆,
∴∠HFD=∠G;在△HFD与△HGB中,
,
∴△HFD≌△HGB(AAS),
∴DF=BG;
在△EGD与△EBD中,
,
∴△EGD≌△EBD(ASA),
∴EG=BE,
∴DF=2BE
 解:CD=2BE;理由如下:如图1,∵∠BAC=90°,
解:CD=2BE;理由如下:如图1,∵∠BAC=90°,∠E=90°,
∴∠FED+∠FAD=180°,
∴A、F、E、D四点共圆,
∴∠ADC=∠F;在△ADC与△AFB中,
|
∴△ADC≌△AFB(AAS),
∴DC=BF;
在△EFC与△EBC中,
|
∴△EFC≌△EBC(ASA),
∴EF=BE,
∴CD=2BE.
(2)DF=2BE.理由如下:
如图,作DG∥AC,交BE的延长线于点G;
则∠BDG=∠C;
∵∠EDB=
| 1 |
| 2 |
∴DE平分∠BDG;
∵DG∥AC,
∴∠BHD=∠A=90°,
而∠HBD=45°,故∠HDB=45°,
∴BH=DH;
∵∠GEF+∠GHF=180°,
∴G、E、F、H四点共圆,
∴∠HFD=∠G;在△HFD与△HGB中,
|
∴△HFD≌△HGB(AAS),
∴DF=BG;
在△EGD与△EBD中,
|
∴△EGD≌△EBD(ASA),
∴EG=BE,
∴DF=2BE
点评:该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是作辅助线,构造全等三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
甲队有工人272人,乙队有工人196人,如果要求乙队的人数是甲队人数的
,应从乙队调多少人去甲队.如果设应从乙队调x人到甲队,列出的方程正确的是( )
| 1 |
| 3 |
A、272+x=
| ||
B、
| ||
C、
| ||
D、
|
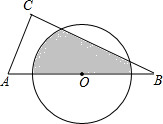 如图,在△ABC中,∠C=90°,AB=6,AC=3,O为AB中点,则半径为
如图,在△ABC中,∠C=90°,AB=6,AC=3,O为AB中点,则半径为 画出图中长方体的正投影.
画出图中长方体的正投影.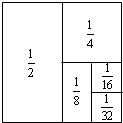 如图所示,将面积为1的长方形等分成两个面积为
如图所示,将面积为1的长方形等分成两个面积为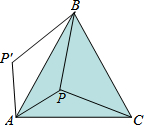 如图,P是正三角形ABC内一点,PA=5,PB=12,PC=13,若三角形PAC绕点A逆时针旋转后,得到三角形P′AB,则∠APB=
如图,P是正三角形ABC内一点,PA=5,PB=12,PC=13,若三角形PAC绕点A逆时针旋转后,得到三角形P′AB,则∠APB=