题目内容
18．
如图，由四个边长为1的正方形构成的田字格，只用没有刻度的直尺在田字格中最多可以作长为$\sqrt{5}$的线段（ ）| A． | 4条 | B． | 6条 | C． | 7条 | D． | 8条 |
分析 结合图形，得到1，2，$\sqrt{5}$是一组勾股数，如图所示，找出长度为$\sqrt{5}$的线段即可．
解答 
解：根据勾股定理得：$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
即1，2，$\sqrt{5}$是一组勾股数，
如图所示，在这个田字格中最多可以作出8条长度为$\sqrt{5}$的线段．
故选D．
点评 此题考查了勾股定理，熟练掌握勾股定理是解本题的关键．
练习册系列答案
口算题天天练系列答案
相关题目
8．某科技小组制作了一个机器人，它能根据指令要求进行行走和旋转，某一指令规定：机器人先向前行走2米，然后左转45°，若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了（ ）
| A． | 14米 | B． | 15米 | C． | 16米 | D． | 17米 |
6．
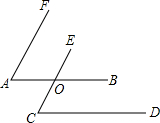如图，∠FAB与∠ECD都是锐角，其中AB∥CD，AF∥CE，射线AB与CE相交于点O，若∠FAB=60°，则∠ECD的度数是（ ）
如图，∠FAB与∠ECD都是锐角，其中AB∥CD，AF∥CE，射线AB与CE相交于点O，若∠FAB=60°，则∠ECD的度数是（ ）| A． | 30° | B． | 60° | C． | 80° | D． | 120° |
13．边长为1的正六边形的内切圆的半径为（ ）
| A． | 2 | B． | 1 | C． | $\underset{\frac{1}{2}}{\;}$ | D． | $\frac{\sqrt{3}}{2}$ |
3．下列多项式的乘法，可以利用平方差公式计算的是（ ）
| A． | （a-b）（b-a） | B． | （-1-a）（a+1） | C． | （-m+n）（-m-n） | D． | （ax+b）（n-bx） |
快、慢两车分别从相距480km的甲、乙两地同时出发，匀速行驶，先相向而行，途中慢车因故停留了1小时，然后继续以原速驶向甲地，到达甲地后即停止行驶；快车到达乙地后，立即按原路原速返回甲地（调头时间忽略不计）．如图是快、慢两车距乙地路程y（km）与所用时间x（h）之间的函数图象，结合图象解答下列问题：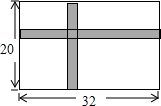
校生物小组有一块长32m，宽20m的矩形实验田，为了管理方便，准备沿平行于两边的方向纵、横个开辟一条等宽的小道，要使种植面积为540m2，小道的宽应是2米．
如图，正方形ABCD的边长为a，面积为6；正方形CEFG的边长为b，面积为2．求△BDF的面积．