题目内容
13.边长为1的正六边形的内切圆的半径为( )| A. | 2 | B. | 1 | C. | $\underset{\frac{1}{2}}{\;}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 根据题意画出图形,利用正六边形中的等边三角形的性质求解即可.
解答 解:如图,连接OA、OB,OG;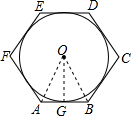
∵六边形ABCDEF是边长为1的正六边形,
∴△OAB是等边三角形,
∴OA=AB=1,
∴OG=OA•sin60°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
∴边长为a的正六边形的内切圆的半径为$\frac{\sqrt{3}}{2}$.
故选D.
点评 此题主要考查正多边形的计算问题,属于常规题,正多边形的计算常用的方法是转化为直角三角形或等腰三角形的计算.

练习册系列答案
相关题目
4. 如图,AE是∠BAC的平分线,DE∥AC交AB于点D.∠1=28°,∠BAE的度数为( )
如图,AE是∠BAC的平分线,DE∥AC交AB于点D.∠1=28°,∠BAE的度数为( )
 如图,AE是∠BAC的平分线,DE∥AC交AB于点D.∠1=28°,∠BAE的度数为( )
如图,AE是∠BAC的平分线,DE∥AC交AB于点D.∠1=28°,∠BAE的度数为( )| A. | 56° | B. | 28° | C. | 18° | D. | 14° |
1.若某同学在一次综合性测试中,语文、数学、英语、科学、社会5门学科的名次在其所在班级里都不超过3(记第一名为1,第二名为2,第三名为3,以此类推且没有并列名次情况),则称该同学为超级学霸.现根据不同班级的甲、乙、丙、丁四位同学对一次综合性测试名次数据的描述,一定可以推断是超级学霸的是( )
| A. | 甲同学:平均数为2,中位数为2 | B. | 乙同学:中位数是2,唯一的众数为2 | ||
| C. | 丙同学:平均数是2,标准差为2 | D. | 丁同学:平均数为2,唯一的众数为2 |
18. 如图,由四个边长为1的正方形构成的田字格,只用没有刻度的直尺在田字格中最多可以作长为$\sqrt{5}$的线段( )
如图,由四个边长为1的正方形构成的田字格,只用没有刻度的直尺在田字格中最多可以作长为$\sqrt{5}$的线段( )
 如图,由四个边长为1的正方形构成的田字格,只用没有刻度的直尺在田字格中最多可以作长为$\sqrt{5}$的线段( )
如图,由四个边长为1的正方形构成的田字格,只用没有刻度的直尺在田字格中最多可以作长为$\sqrt{5}$的线段( )| A. | 4条 | B. | 6条 | C. | 7条 | D. | 8条 |
5.以下列长度为三角形边长,不能构成直角三角形的是( )
| A. | 15,112,113 | B. | 4,5,6 | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 45,$\sqrt{10}$,$\sqrt{2015}$ |
2.要使二次根式$\sqrt{x+5}$有意义,则x的取值范围是( )
| A. | x>-5 | B. | x≥-5 | C. | x≤-5 | D. | x≠-5 |
 已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:
已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法: 某校在“爱护水资源”活动中组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布条形图.已知从左至右4个小组的频率分别是0.05,0.15,0.35,0.30.那么在这次评比中,被评为优秀的调查报告有(分数大于或等于80分为优秀,且分数为整数)( )
某校在“爱护水资源”活动中组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布条形图.已知从左至右4个小组的频率分别是0.05,0.15,0.35,0.30.那么在这次评比中,被评为优秀的调查报告有(分数大于或等于80分为优秀,且分数为整数)( )