题目内容
13．已知∠A：∠B：∠C=5：2：7，则△ABC的形状是（ ）| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 无法确定形状 |
分析 根据比例设∠A、∠B、∠C分别为5k、2k、7k，然后利用三角形的内角和定理，列出方程求出最大角的度数，判断三角形的形状．
解答 解：设∠A、∠B、∠C分别为5k、2k、7k，
则5k+2k+7k=180°，
解得7k=90°，
即∠C=90°，
∴△ABC是直角三角形．
故选：B．
点评 本题考查了三角形的内角和定理：三角形内角和是180°．利用“设k法”求解更简便．
练习册系列答案
名校课堂系列答案
相关题目
3．
如图，已知△ABC中，AD=BD，AC=4，H是高AD和BE的交点，则线段BH的长度为（ ）
如图，已知△ABC中，AD=BD，AC=4，H是高AD和BE的交点，则线段BH的长度为（ ）| A． | $\sqrt{6}$ | B． | 4 | C． | 2$\sqrt{3}$ | D． | 5 |
如图，点C、B、E在同一条直线上，AB∥DE，∠ACB=∠CDE，AC=CD，求证：AB=CE．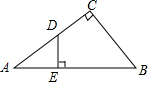
在△ABC中，∠ACB=90°，DE⊥AB．
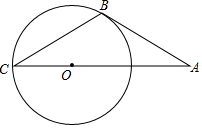如图，直线AB是⊙O的切线，B为切点，AO的延长线交⊙O于点C，且∠A=30°，试判断AB与BC的大小关系．