题目内容
3.根据条件,求下列二次函数的解析式.(1)函数y=(m-3)x2+mx+(m+3)的最大值为0;
(2)抛物线y=x2-5(m+1)x+2m的对称轴是y轴.
分析 (1)根据二次函数y=ax2+bx+c(a≠0),当a<0,x=-$\frac{b}{2a}$时,y有最大值$\frac{4ac-{b}^{2}}{4a}$得到m-3<0,且$\frac{4(m-3)(m+3)-{m}^{2}}{4(m-3)}$=0,化简得m2-12=0,然后解方程得m1=2$\sqrt{3}$,m2=-2$\sqrt{3}$,最后确定满足条件的m的值.
(2)由对称轴是y轴可知一次项系数为0,可求得m的值.
解答 解:(1)a=m-3,b=m,c=m+3,
∵二次函数有最大值为0,
∴a<0即m-3<0,且$\frac{4ac-{b}^{2}}{4a}$=0,
即$\frac{4(m-3)(m+3)-{m}^{2}}{4(m-3)}$=0,
化简得m2-12=0,m1=2$\sqrt{3}$,m2=-2$\sqrt{3}$,
∵m<3,
∴m=-2$\sqrt{3}$.
故二次函数的解析式为:y=(-2$\sqrt{3}$-3)x2-2$\sqrt{3}$x-2$\sqrt{3}$+3).
(2)∵抛物线y=x2-5(m+1)x+2m的对称轴是y轴,
∴m+1=0,解得m=-1,
故二次函数的解析式为:y=x2-2.
点评 本题考查了二次函数的最值问题:二次函数y=ax2+bx+c(a≠0),当a>0,x=-$\frac{b}{2a}$时,y有最小值$\frac{4ac-{b}^{2}}{4a}$;当a<0,x=-$\frac{b}{2a}$时,y有最大值$\frac{4ac-{b}^{2}}{4a}$;也考查抛物线的对称轴,掌握抛物线的对称轴为y轴其一次项系数为0是解题的关键..

练习册系列答案
相关题目
13.已知∠A:∠B:∠C=5:2:7,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定形状 |
9.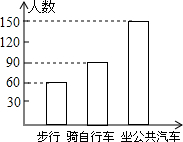 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | 步行人数最少,只为90人 | |
| B. | 步行人数为50人 | |
| C. | 步行与骑自行车的人数和比坐公共汽车的人数要多 | |
| D. | 坐公共汽车的人数占总数的50% |
10. 如图几何体从正面看是( )
如图几何体从正面看是( )
 如图几何体从正面看是( )
如图几何体从正面看是( )| A. |  | B. |  | C. |  | D. |  |
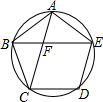 如图所示,正五边形ABCDE的对角线AC和BE相交于点F,求证:AC=AB+BF.
如图所示,正五边形ABCDE的对角线AC和BE相交于点F,求证:AC=AB+BF.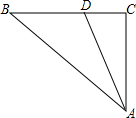 Rt△ABC中,∠C=90°,AC=3,BC=4,动点D在边BC上从点C向点B运动,连接AD,点C关于直线AD的对称点为点P,若△BCP为等腰三角形,则CP2的值为16或18-6$\sqrt{5}$或$\frac{576}{25}$.
Rt△ABC中,∠C=90°,AC=3,BC=4,动点D在边BC上从点C向点B运动,连接AD,点C关于直线AD的对称点为点P,若△BCP为等腰三角形,则CP2的值为16或18-6$\sqrt{5}$或$\frac{576}{25}$. 如图,在△ABC中,∠B>∠C,AE、AD分别是∠A的平分线和BC边上的高.求证:∠DAE=$\frac{1}{2}$(∠B-∠C).
如图,在△ABC中,∠B>∠C,AE、AD分别是∠A的平分线和BC边上的高.求证:∠DAE=$\frac{1}{2}$(∠B-∠C).