题目内容
2.(1)(π-3.14)0+(sin30°)-1+|-4cos45°|-$\sqrt{8}$(2)解方程组:$\left\{\begin{array}{l}{3x-5y=3}\\{\frac{x}{2}-\frac{y}{3}=1}\end{array}\right.$.
分析 (1)本题涉及零指数幂、负整数指数幂、特殊角的三角函数值、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
(2)先将方程组整理为一般形式,再根据加减消元法解二元一次方程组即可求解
解答 解:(1)(π-3.14)0+(sin30°)-1+|-4cos45°|-$\sqrt{8}$
=1+2+2$\sqrt{2}$-2$\sqrt{2}$
=3;
(2)$\left\{\begin{array}{l}{3x-5y=3}\\{\frac{x}{2}-\frac{y}{3}=1}\end{array}\right.$,
方程组整理得$\left\{\begin{array}{l}{3x-5y=3①}\\{3x-2y=6②}\end{array}\right.$,
②-①得:3y=3,解得y=1,
将y=1代入①得:x=$\frac{8}{3}$.
故原方程组的解为$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=1}\end{array}\right.$.
点评 本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.同时考查了加减消元法解二元一次方程组.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.把抛物线y=-2x2的图象向左平移4个单位,再向上平移3个单位,所得的图象的表达式( )
| A. | y=-2(x+4)2+3 | B. | y=-2(x-4)2-3 | C. | y=-2(x+4)2-3 | D. | y=-2(x-4)2+3 |
11.下列各式中,无论x取何实数值,分式都有意义的是( )
| A. | $\frac{x}{x+1}$ | B. | $\frac{1}{x-1}$ | C. | $\frac{{x}^{2}+1}{{x}^{2}}$ | D. | $\frac{{x}^{2}}{{x}^{2}+1}$ |
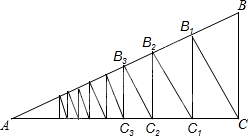 如图,在Rt△ABC中,BC⊥AC,∠BAC=30°,CB1⊥AB,B1C1⊥AC,C1B2⊥AB,B2C2⊥AC…以此类推,若BC=a,则BnCn=($\frac{3}{4}$)na.
如图,在Rt△ABC中,BC⊥AC,∠BAC=30°,CB1⊥AB,B1C1⊥AC,C1B2⊥AB,B2C2⊥AC…以此类推,若BC=a,则BnCn=($\frac{3}{4}$)na.