Question

12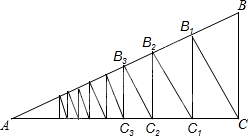．如图，在Rt△ABC中，BC⊥AC，∠BAC=30°，CB₁⊥AB，B₁C₁⊥AC，C₁B₂⊥AB，B₂C₂⊥AC…以此类推，若BC=a，则B_nC_n=（$\frac{3}{4}$）ⁿa．

Answer 1

分析 根据BC⊥AC，B₁C₁⊥AC，得到BC∥B₁C₁，得到∠C₁B₁C=30°，根据余弦的概念求出B₁C₁的值，同理得到B₂C₂的值，根据规律得到答案．

解答 解：∵BC⊥AC，B₁C₁⊥AC，
∴BC∥B₁C₁，
∴∠C₁B₁C=30°，
∴B₁C₁=BC•cos30°•cos30°=$\frac{3}{4}$a，
同理B₂C₂=B₁C₁•cos30°•cos30°=（$\frac{3}{4}$）²a，
∴B_nC_n=（$\frac{3}{4}$）ⁿa，
故答案为：（$\frac{3}{4}$）ⁿa．

点评 本题考查的是锐角三角函数的概念和特殊角的三角函数值，掌握锐角三角函数的概念是解题的关键．