题目内容
12.一个三角形三边长之比为4:5:6,三边中点连线组成的三角形的周长为30cm,则原三角形最大边长为( )| A. | 44厘米 | B. | 40厘米 | C. | 36厘米 | D. | 24厘米 |
分析 根据△DEF的周长为30cm、三边长之比为4:5:6,求得最长边为12,则由三角形中位线定理知,原△ABC的最长边的边长为24.
解答 解:如图, 点D、E、F分别是边AB、BC、AC上的中点,EF:DE:DF=4:5:6,△DEF的周长为30cm.
点D、E、F分别是边AB、BC、AC上的中点,EF:DE:DF=4:5:6,△DEF的周长为30cm.
∵EF:DE:DF=4:5:6,EF+DE+DF=30cm,
∴EF=8cm,DE=10cm,DF=12cm.
∵点D、E分别是边AB、BC边上的中点,
∴DE是△ABC的中位线,
∴DE=$\frac{1}{2}$AC,即AC=2DE=20cm.
同理求得AB=2EF=16cm,BC=2DF=24cm,
∵24cm>20cm>16cm,
∴原三角形最大边长为24cm.
故选:D.
点评 本题考查了三角形中位线定理.此题考查的是三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
相关题目
10.从多边形的一个顶点出发向其余的顶点引对角线,将多边形分成10个三角形,则此多边形的边数为( )
| A. | 9 | B. | 11 | C. | 12 | D. | 10 |
17.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.下列四组数中不能构成直角三角形的一组是( )
| A. | 1,2,$\sqrt{6}$ | B. | 3,5,4 | C. | 5,12,13 | D. | 3,2,$\sqrt{13}$ |
 ∠ACB=∠ADC=90°,AC=3,CD=2.当AB的长为$\frac{9\sqrt{5}}{5}$或$\frac{9}{2}$时,这两个直角三角形相似.
∠ACB=∠ADC=90°,AC=3,CD=2.当AB的长为$\frac{9\sqrt{5}}{5}$或$\frac{9}{2}$时,这两个直角三角形相似.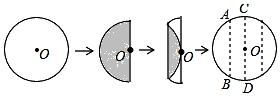 把一张圆形纸片按如图方式折叠两次后展开,图中的虚线表示折痕,则弧$\widehat{BC}$的度数是150°.
把一张圆形纸片按如图方式折叠两次后展开,图中的虚线表示折痕,则弧$\widehat{BC}$的度数是150°.