Question

10．已知点P是正方形ABCD的边BC上任一点（不与B、C重合），分别过点B、C作BE⊥DP、CF⊥DP，垂足分别为E、F．

（1）如图1，图中是否存在与CF相等的线段？若存在，请找出，并加以证明，若不存在，说明理由；
（2）如图2，若点P是CB延长线上一点，其他条件不变，BE、EF、DF三条线段之间有怎样的数量关系？请证明你的结论．

Answer 1

分析 （1）先过点B作BG⊥CF，交CF的延长线于G，构造矩形BEFG，根据矩形的性质以及正方形的性质，判定△BCG≌△CDF，进而根据EF=BG和BG=CF得出结论；
（2）先过点B作BG⊥CF于点G，构造矩形BEFG，根据矩形的性质以及正方形的性质，判定△BCG≌△CDF，进而根据EF=CF，BE=FG，FG+CG=CF得出结论．

解答 解：（1）存在EF=CF．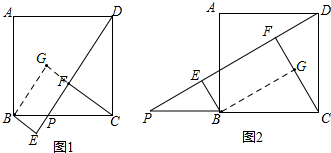
理由：过点B作BG⊥CF，交CF的延长线于G，
又∵BE⊥DP，CF⊥DP，
∴四边形BGFE是矩形，且∠DCF+∠FDC=90°，
∴EF=BG，∠G=∠CFD=90°，
∵正方形ABCD中，CB=DC，∠BCD=90°，
∴∠BCG+∠DCF=90°，
∴∠BCG=∠FDC，
由∠G=∠CFD，∠BCG=∠FDC，CB=DC可得：△BCG≌△CDF（AAS），
∴BG=CF，
∴EF=CF；

（2）BE+DF=EF．
理由：过点B作BG⊥CF于点G，
又∵BE⊥DP，CF⊥DP，
∴四边形BGFE是矩形，且∠DCF+∠FDC=90°，
∴EF=BG，BE=FG，∠BGC=∠CFD=90°，
∵正方形ABCD中，CB=DC，∠BCD=90°，
∴∠BCG+∠DCF=90°，
∴∠BCG=∠FDC，
由∠BGC=∠CFD，∠BCG=∠FDC，CB=DC可得：△BCG≌△CDF（AAS），
∴BG=CF，CG=DF，
∴EF=CF，
又∵FG+CG=CF，
∴BE+DF=EF．

点评 本题主要考查了正方形的性质以及矩形的性质，解决问题的关键是作辅助线构造全等三角形，根据全等三角形的对应边相等，以及矩形的对边相等得出结论．