题目内容
18．已知用配方法解关于x的一元二次方程ax2-2abx-ab2=7，所得的两根为$\frac{1}{2}±\frac{1}{2}\sqrt{7}$，求a+b的值．分析 由方程的两根结合根与系数的关系，即可得出关于a、b的方程组，解之即可得出a、b值，将其相加即可得出结论．
解答 解：∵关于x的一元二次方程ax2-2abx-ab2=7的两根为$\frac{1}{2}±\frac{1}{2}\sqrt{7}$，
∴$\left\{\begin{array}{l}{2b=1}\\{-\frac{a{b}^{2}+7}{a}=-\frac{3}{2}}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=\frac{28}{5}}\\{b=\frac{1}{2}}\end{array}\right.$，
∴a+b=$\frac{28}{5}$+$\frac{1}{2}$=$\frac{61}{10}$．
点评 本题考查了根与系数的关系，根据方程的两根结合根与系数的关系找出关于a、b的方程组是解题的关键．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
相关题目
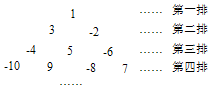将整数1，-2，3，-4，5，-6，…按如图所示的规律排列下去，若有序实数对（n，m）表示第n排，从左到右第m个数，如（4，2）表示实数9，则表示实数2017的有序实数对是（64，64）．
13．已知Rt△ABC中，∠A=90°，∠B=30°，CD平分∠ACB且与AB边交于点D，AC=$\sqrt{6}$，则点D到边BC的距离是（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\sqrt{6}$ |
将n个边长都为2的正方形按如图所示摆放，点A1，A2，…，An分别是正方形的中心，则这n个正方形重叠部分的面积之和是n-1．