题目内容
10．
将n个边长都为2的正方形按如图所示摆放，点A1，A2，…，An分别是正方形的中心，则这n个正方形重叠部分的面积之和是n-1．
分析 根据题意可得，阴影部分的面积是正方形的面积的$\frac{1}{4}$，已知两个正方形可得到一个阴影部分，则n个这样的正方形重叠部分即为（n-1）个阴影部分的和．
解答 解：由题意可得一个阴影部分面积等于正方形面积的$\frac{1}{4}$，即是$\frac{1}{4}$×4=1，
n个这样的正方形重叠部分（阴影部分）的面积和为：1×（n-1）=n-1．
故答案为：n-1．
点评 此题考查了正方形的性质，解决本题的关键是得到n个这样的正方形重叠部分（阴影部分）的面积和的计算方法，难点是求得一个阴影部分的面积．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
相关题目
1．下列说法正确的是（ ）
| A． | 点P（2，-3）在第二象限 | |
| B． | 点M（3，-4）到x轴的距离为3 | |
| C． | 如果点P（a，b）在x轴上，那么a=0 | |
| D． | 如果A（-2，3），B（-2，-3），那么直线AB∥y轴 |
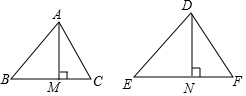相似三角形面积的比等于相似比的平方，相似多边形面积之比等于相似比的平方．
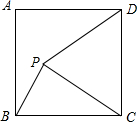如图，正方形ABCD的边长为4，点P为正方形内部（含边上）的任意一点，且BP=2，分别连接PC、PD，则PD+$\frac{1}{2}$PC的最小值为5．
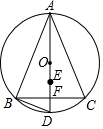如图，在△ABC中，AB=AC，AD⊥BC于点F，交△ABC外接圆于点D，BC=6，tan∠BAC=$\frac{3}{4}$，点E是△ABC内切圆的圆心，则OE的长为5-$\sqrt{10}$．
在Rt△ABC中，AB=BC，∠ABC=90°，以AB为直径作半圆O，P是BC边上一动点（不与B、c重合），过点P作半圆O的切线，与过A点的垂线交于点Q．AC与PQ，OQ分别交于点E，F，如果P，C，F三点构成的三角形与△AEO相似，那么∠CPF的度数是90°或60°．