题目内容
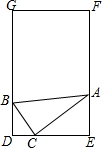 刘敏将一个直角三角板如图放置在一门框内,使得三角板的三个顶点恰好落在门框的三个边上,且点B距门框底端内缘0.4m,其中∠BAC=30°,∠ACB=90°,∠ACE=37°.
刘敏将一个直角三角板如图放置在一门框内,使得三角板的三个顶点恰好落在门框的三个边上,且点B距门框底端内缘0.4m,其中∠BAC=30°,∠ACB=90°,∠ACE=37°.(1)求出三角板的斜边长;
(2)请你帮刘敏计算此门框的外宽度DE.(门框边缘厚为0.08m,计算结果精确到0.1m,可使用科学计算器,参考数据:sin37°≈0.60,cos37°≈0.80.tan37≈0.75,
| 3 |
考点:解直角三角形的应用
专题:
分析:(1)利用锐角三角函数关系得出BC的长,进而利用直角三角形中30°所对的边是斜边的一半,求出AB即可;
(2)首先求出CD的长,即可利用锐角三角函数关系得出AC,CE的长,进而得出答案.
(2)首先求出CD的长,即可利用锐角三角函数关系得出AC,CE的长,进而得出答案.
解答:解:(1)∵∠BAC=30°,∠ACB=90°,
∴BC=
AB,
∵∠ACE=37°,∠ACB=90°,
∴∠BCD=53°,∠DBC=37°,
∴cos37°=
=
=0.80,
解得:BC=0.5,
∴AB=2BC=1(m);
(2)∵BD=0.4m,BC=0.5m,
∴CD=0.3m,
∵AC=ABcos30°=
≈0.865(m),
CE=ACcos37°≈0.692(m),
DE=0.3+0.992+0.08×2=1.152≈1.2(m),
答:门框的外宽度DE为1.2m.
∴BC=
| 1 |
| 2 |
∵∠ACE=37°,∠ACB=90°,
∴∠BCD=53°,∠DBC=37°,
∴cos37°=
| BD |
| BC |
| 0.4 |
| BC |
解得:BC=0.5,
∴AB=2BC=1(m);
(2)∵BD=0.4m,BC=0.5m,
∴CD=0.3m,
∵AC=ABcos30°=
| ||
| 2 |
CE=ACcos37°≈0.692(m),
DE=0.3+0.992+0.08×2=1.152≈1.2(m),
答:门框的外宽度DE为1.2m.
点评:此题主要考查了解直角三角形的应用,根据题意熟练利用锐角三角函数关系是解题关键.

练习册系列答案
相关题目
在平面直角坐标系中,下列结论成立的是( )
| A、点(1,2)和点(2,1)表示同一个点 |
| B、平面内任一点到两坐标轴的距离相等 |
| C、点P的坐标(m,n)满足mn=0,则点P在坐标轴上 |
| D、点M(a,-2)到y轴的距离是a |
 如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地.
如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地.
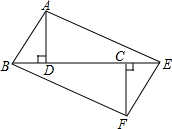 如图,已知Rt△ABD≌Rt△FEC,且B、D、C、E在同一直线上,连接BF、AE.
如图,已知Rt△ABD≌Rt△FEC,且B、D、C、E在同一直线上,连接BF、AE. 如图,在△ABC中,AC=BC,∠ACB=90°,D为AC延长线上一点,点E在BC边上,且CE=CD,连结AE、BD、DE.
如图,在△ABC中,AC=BC,∠ACB=90°,D为AC延长线上一点,点E在BC边上,且CE=CD,连结AE、BD、DE.