题目内容

已知a-b=3，b-c=1，a2+b2+c2=30，求ab+bc+ac的值．
考点：完全平方公式
专题：计算题
分析：由a-b与b-c的值，求出a-c的值，利用完全平方公式得到（a-b）2+（b-c）2+（a-c）2=2（a2+b2+c2）-2（ab+ac+bc），将各自的值代入计算即可求出ab+bc+ac的值．
解答：解：∵a-b=3，b-c=1，∴a-c=4，
∵（a-b）2+（b-c）2+（a-c）2=2（a2+b2+c2）-2（ab+ac+bc），
∴2（ab+bc+ac）=2（a2+b2+c2）-[（a-b）2+（b-c）2+（a-c）2]，
∵a2+b2+c2=30，
∴ab+bc+ac=17．
点评：此题考查了完全平方公式，熟练掌握公式是解本题的关键．
练习册系列答案
相关题目
下列各式成立的是（　　）
A、
16
=±4
B、±
36
=6
C、
(-2)2
=-2
D、
3-27
=-3
如图，已知△ABC中，AB=AC，D为△ABC所在平面内的一点，过D作DE∥AB，DF∥AC分别交直线AC、直线AB于点E、F．

（1）如图1，当点D在线段BC上时，通过观察分析线段DE、DF、AB之间的数量关系，并说明理由；
（2）如图2，当点D在直线BC上，其它条件不变时，试猜想线段DE、DF、AB之间的数量关系（请直接写出等式，不需证明）；
（3）如图3，当点D是△ABC内一点，过D作DE∥AB，DF∥AC分别交直线AC、直线AB和直线BC于E、F和G．试猜想线段DE、DF、DG与AB之间的数量关系（请直接写出等式，不需证明）．
在学习三角形中线的知识时，小明了解到：三角形的任意一条中线所在的直线可以把该三角形分为面积相等的两部分．进而，小明继续研究，过四边形的某一顶点的直线能否将该四边形平分为面积相等的两部分？他画出了如下示意图（如图1），得到了符合要求的直线AF．
小明的作图步骤如下：
第一步：连结AC；
第二步：过点B作BE∥AC交DC的延长线于点E；
第三步：取ED中点F，作直线AF；
则直线AF即为所求．
请参考小明思考问题的方法，解决问题：
如图2，五边形ABOCD，各顶点坐标为：A（3，4），B（0，2），O（0，0），C（4，0），D（4，2）．请你构造一条经过顶点A的直线，将五边形ABOCD分为面积相等的两部分，并求出该直线的解析式．
暑假期间，两位家长计划带领若干名学生去旅游，他们联系了报价均为每人1000元的两家旅行社．经协商，甲旅行社的优惠条件是：两位家长全额收费，学生都按7折收费；乙旅行社的优惠条件是：学生、家长都按8折收费．假设这两位家长带领x名学生去旅行，甲、乙旅行社的收费分别为y甲、y乙，
（1）写出y甲、y乙与x的函数关系式．
（2）学生人数在什么情况下，选择甲旅行社更省钱？
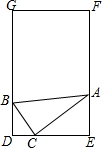刘敏将一个直角三角板如图放置在一门框内，使得三角板的三个顶点恰好落在门框的三个边上，且点B距门框底端内缘0.4m，其中∠BAC=30°，∠ACB=90°，∠ACE=37°．
（1）求出三角板的斜边长；
（2）请你帮刘敏计算此门框的外宽度DE．（门框边缘厚为0.08m，计算结果精确到0.1m，可使用科学计算器，参考数据：sin37°≈0.60，cos37°≈0.80．tan37≈0.75，
3
=1.73）
计算：
（1）（
24
-
2
）-（
8
+
6
）；
（2）（2
7
-5
2
）2-（5
2
+2
7
）2．
（4b
a
b
+
2
a
a3b
）-（3a
b
a
+
9ab
）（a＞0，b＞0）
填写推理理由，如图，已知AD⊥BC于D，EF⊥BC于F，AD平分∠BAC．将∠E=∠1的过程填写完整．
解：解：∵AD⊥BC，EF⊥BC（ 已知 ）
∴∠ADC=∠EFC=90°（ 垂直的意义 ）
∴AD∥EF
∴∠1=
 

∠E=
 

又∵AD平分∠BAC（已知）
∴
 
=
 

∴∠1=∠E．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网