题目内容
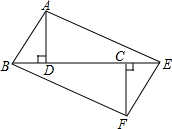 如图,已知Rt△ABD≌Rt△FEC,且B、D、C、E在同一直线上,连接BF、AE.
如图,已知Rt△ABD≌Rt△FEC,且B、D、C、E在同一直线上,连接BF、AE.(1)求证:四边形ABFE是平行四边形.
(2)若∠ABD=60°,AB=2cm,DC=4cm,将△ABD沿着BE方向以1cm/s的速度运动,设△ABD运动的时间为t,在△ABD运动过程中,试解决以下问题:
(1)当四边形ABEF是菱形时,求t的值;
(2)是否存在四边形ABFE是矩形的情形?如果存在,求出t的值,如果不存在,请说明理由.
考点:矩形的判定,全等三角形的判定与性质,平行四边形的判定,菱形的判定
专题:动点型
分析:(1)根据全等三角形的对应角相等、对应边的比相等得到AB平行且等于EF,利用一组对边平行且相等的四边形是平行四边形判定即可;
(2)①根据菱形的对角线的性质得到当点C和点D重合时,四边形ABFE是菱形,求出此时t的值即可;
②当四边形ABFE是矩形时,∠BAE=90°,根据矩形的性质求得线段CD的长,从而求得t的值.
(2)①根据菱形的对角线的性质得到当点C和点D重合时,四边形ABFE是菱形,求出此时t的值即可;
②当四边形ABFE是矩形时,∠BAE=90°,根据矩形的性质求得线段CD的长,从而求得t的值.
解答: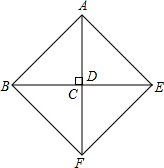 解:(1)∵Rt△ABD≌Rt△FEC,
解:(1)∵Rt△ABD≌Rt△FEC,
∴AB=EF,∠ABD=∠FEC,
∴AB∥EF,
∴平行四边形ABFE是平行四边形;
(2)①如图,当点D与点C重合时,四边形ABFE是菱形,
此时△ABD运动的距离为4cm,
∴t=4;
②存在
当四边形ABFE是矩形时,∠BAE=90°,
∴∠BAE=90°-60°=30°,
∵AB=2cm,
∴BE=4cm,BD=1cm,
∴CD=4-1-1=2cm,
∴t=2.
 解:(1)∵Rt△ABD≌Rt△FEC,
解:(1)∵Rt△ABD≌Rt△FEC,∴AB=EF,∠ABD=∠FEC,
∴AB∥EF,
∴平行四边形ABFE是平行四边形;
(2)①如图,当点D与点C重合时,四边形ABFE是菱形,
此时△ABD运动的距离为4cm,
∴t=4;
②存在
当四边形ABFE是矩形时,∠BAE=90°,
∴∠BAE=90°-60°=30°,
∵AB=2cm,
∴BE=4cm,BD=1cm,
∴CD=4-1-1=2cm,
∴t=2.
点评:本题考查了平行四边形的判定、矩形的判定、菱形的判定等知识,综合性较强,但难度不算很大.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
下列事件是必然事件的是( )
| A、打开电视机,屏幕上正在播放天气预报 |
| B、在地球上,抛出去的篮球会下落 |
| C、到电影院任意买一张电影票,座位号是奇数 |
| D、掷一枚均匀的骰子,向上一面的点数为偶数 |

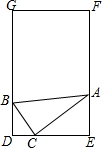 刘敏将一个直角三角板如图放置在一门框内,使得三角板的三个顶点恰好落在门框的三个边上,且点B距门框底端内缘0.4m,其中∠BAC=30°,∠ACB=90°,∠ACE=37°.
刘敏将一个直角三角板如图放置在一门框内,使得三角板的三个顶点恰好落在门框的三个边上,且点B距门框底端内缘0.4m,其中∠BAC=30°,∠ACB=90°,∠ACE=37°. 如图,在Rt△ABC中,∠C=90°,∠B=60°,内切圆O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为
如图,在Rt△ABC中,∠C=90°,∠B=60°,内切圆O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为