题目内容
13.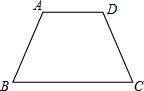 如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=7,BC=12,求∠B的度数.
如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=7,BC=12,求∠B的度数.
分析 过A作AE∥DC交BC于E,得出四边形ADCE是平行四边形,根据平行四边形的性质得出AE=DC,AD=EC,求出AB=DC=AE=7,EC=AD=5,BE=7,根据等边三角形的判定得出△ABE是等边三角形,即可得出答案.
解答 解:过A作AE∥DC交BC于E,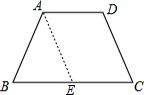
∵AD∥BC,
∴四边形ADCE是平行四边形,
∴AE=DC,AD=EC,
∵四边形ABCD是等腰梯形,AD∥BC,AD=5,AB=7,BC=12,
∴AB=DC=AE=7,EC=AD=5,
∴BE=12-5=7,
∴AB=AE=BE,
∴△ABE是等边三角形,
∴∠B=60°.
点评 本题考查了等腰梯形的性质,平行四边形的性质和判定,等边三角形的性质和判定的应用,能正确作辅助线是解此题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
2.当x=( )时,|x+6|有最( )值,是( )
| A. | 0,大,0 | B. | 0,小,0 | C. | -6,大,0 | D. | -6,小,0 |
 如图,已知点O在直线AB上,0D、0E分别平分∠BOC、∠AOC,∠BOC=80°.
如图,已知点O在直线AB上,0D、0E分别平分∠BOC、∠AOC,∠BOC=80°.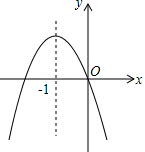 二次函数y=ax2+bx+c的图象如图所示,下列结论:①a+b+c>0;②a-b+c>0;③abc<0;④2a-b=0,其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①a+b+c>0;②a-b+c>0;③abc<0;④2a-b=0,其中正确的个数是( )