题目内容
1. 如图,已知点O在直线AB上,0D、0E分别平分∠BOC、∠AOC,∠BOC=80°.
如图,已知点O在直线AB上,0D、0E分别平分∠BOC、∠AOC,∠BOC=80°.(1)求∠AOD的度数;
(2)∠DOC和∠COE有什么关系?简单说明理由.
(3)若∠BOC=60°,其他条件不变.(2)中的结论还成立吗?
分析 (1)先根据角平分线定义计算出∠BOD=$\frac{1}{2}$∠BOC=40°,然后利用邻补角的定义可计算出∠AOD的度数;
(2)先根据角平分线定义计算出∠DOC=$\frac{1}{2}$∠BOC=40°,再利用邻补角的定义得到∠AOC=180°-∠BOC=100°,则∠COE=$\frac{1}{2}$∠AOC=50°,所以∠DOC+∠COE=90°;
(3)若∠BOC=60°,与(2)的计算方法一样,可得∠DOC+∠COE=90°.
解答 解:(1)∵0D平分∠BOC,
∴∠BOD=$\frac{1}{2}$∠BOC=$\frac{1}{2}×$80°=40°,
∵∠AOB=180°,
∴∠AOD=180°-40°=140°;
(2)∠DOC和∠COE互余.理由如下:
∵0D平分∠BOC,
∴∠DOC=$\frac{1}{2}$∠BOC=$\frac{1}{2}×$80°=40°,
而∠AOC=180°-∠BOC=180°-80°=100°,
∵0E平分∠AOC,
∴∠COE=$\frac{1}{2}$∠AOC=50°,
∴∠DOC+∠COE=50°+40°=90°;
(3)若∠BOC=60°,其他条件不变,(2)中的结论还成立.理由如下:
∵0D平分∠BOC,
∴∠DOC=$\frac{1}{2}$∠BOC=$\frac{1}{2}×$60°=30°,
而∠AOC=180°-∠BOC=180°-60°=120°,
∵0E平分∠AOC,
∴∠COE=$\frac{1}{2}$∠AOC=60°,
∴∠DOC+∠COE=30°+60°=90°.
点评 本题考查了角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.性质:若OC是∠AOB的平分线则∠AOC=∠BOC=$\frac{1}{2}$∠AOB或∠AOB=2∠AOC=2∠BOC.

 名校课堂系列答案
名校课堂系列答案| A. | 2ax2与3x2 | B. | -1和3 | C. | 2xy2和-y2x | D. | 8xy和-8xy |
 如图,铅球投掷场地呈扇形,其中投掷区的角度为40°,则这个角的余角为50°,补角为140°.
如图,铅球投掷场地呈扇形,其中投掷区的角度为40°,则这个角的余角为50°,补角为140°. 一个直棱柱的主视图、俯视图如图所示,请描述这个直棱柱的形状,并补画左视图.
一个直棱柱的主视图、俯视图如图所示,请描述这个直棱柱的形状,并补画左视图.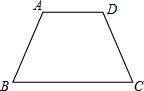 如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=7,BC=12,求∠B的度数.
如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=7,BC=12,求∠B的度数.